2025年高职单招《数学(中职)》每日一练试题04月16日

2025年高职单招《数学(中职)》每日一练试题04月16日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

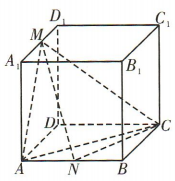
1、如图,已知正方体 ABCD-A₁B₁C₁D₁的体积为1,M,N分别是棱A₁D₁,AB 的中点,则三棱锥M-ANC的体积为（）  

• A：
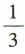
• B：
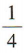
• C：
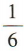
• D：

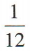
答 案：D

解 析：易知正方体 ABCD - A₁B₁C₁D₁的棱长为1.由题意知三棱锥 M-ANC的高为1,底面三角形 ANC的面积为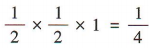,所以三棱锥M-ANC的体积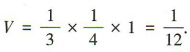

2、下列选项中，与α=-30°终边相同的角是（）

• A：30°角
• B：240°角
• C：300°角
• D：330°角

答 案：D

解 析：与α=-30°终边相同的角表示为θ=-30°+360°·k,k∈Z,当k=1时，θ=330°,所以330°角与α的终边相同.经检验选项A,B,C均不符合题意.

3、若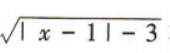有意义，则x的取值范围是（）

• A：(-2,4)
• B：(-∞,-2)∪(4,+∞)
• C：[-2,4]
• D：(-∞,-2]∞[4,+∞)

答 案：D

解 析：

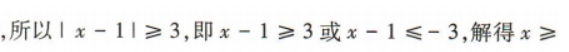
主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、函数f(x)=sin(x+φ)-2sinφcosx的最大值为____________  

答 案：1

解 析：f(x)=sinxcosφ+cosxsinφ-2sinφcosx =sinxcosφ-cosxsinφ =sin(x-φ)≤1， 故函数f(x)=sin(x+φ)-2sinφcosx的最大值为1  

2、（）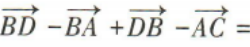  

答 案：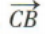

解 析：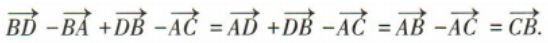

3、某高中学校三个年级共有学生2000名.若在全校学生中随机抽取一名学生,抽到高二年级女生的概率为 0.19,则高二年级的女生人数为()  

答 案：380

解 析：易得高二年级的女生人数为2000x0.19=380.

简答题

1、解关于x的不等式56x²+ax2

答 案：解:将所求不等式转化为56x²+ax-a²<0 令56x²+ax-a²=0,得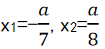 当a>0时,所求不等式的解集为 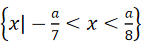当a<0时,所求不等式的解集为