2025年高职单招《数学(中职)》每日一练试题11月05日
2025-11-05 15:52:43 来源:勒克斯教育网
2025年高职单招《数学(中职)》每日一练试题11月05日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、函数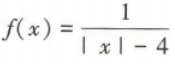 的定义域为()
的定义域为()
- A:{xlx≠0}
- B:{x|x≠-4}
- C:{x|x≠4}
- D:{x|x≠±4}
答 案:D
解 析:要使函数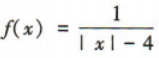 有意义,须|x|-4≠0,即|x|≠4,解得x≠±4,故函数
有意义,须|x|-4≠0,即|x|≠4,解得x≠±4,故函数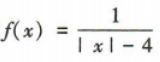 的定义域为{x|x≠±4}.
的定义域为{x|x≠±4}.
2、已知数列{an}为等比数列,若a1=8,a4=64,则公比q等于()
- A:3
- B:-3
- C:2
- D:-2
答 案:C
解 析:由题意得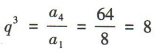 ,所以q=2。
,所以q=2。
3、已知△ABC的内角A,B,C的对边分别为a,b,c,若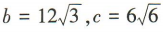 ,B=45°,则C=()
,B=45°,则C=()
- A:30°
- B:105°
- C:150°
- D:30°或105°
答 案:A
解 析:在△ABC中,由 ,得
,得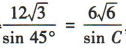 ,解得
,解得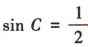 .因为
.因为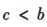 ,所以
,所以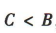 ,所以C=30°.
,所以C=30°.
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、当0<x<1时,x(1-x)取最大值时的值为____________
答 案:x=1/2
解 析:∵0 ;当且仅当x=1-x即x=1/2 时,等号成立
;当且仅当x=1-x即x=1/2 时,等号成立
2、一个数分别加上20,50,100后得到的三个数成等比数列,则这个数为()
答 案:25
解 析:设所求的数为x.根据题意得(x+50)2=(x+20)(x+100),解得x=25.
3、函数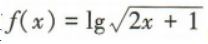 的定义域为()
的定义域为()
答 案: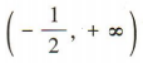
解 析: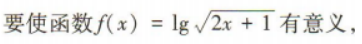
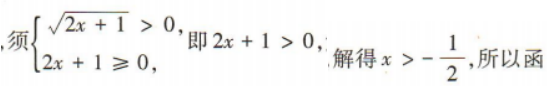
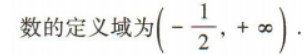
简答题
1、已知椭圆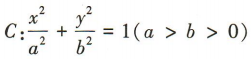 的长轴长为 10,焦距为 6.(1)求椭圆C的方程;
的长轴长为 10,焦距为 6.(1)求椭圆C的方程;
(2)若直线1与C交于A,B两点,且线段AB 的中点为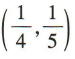 ,求直线l的方程.
,求直线l的方程.
答 案:(1)设C的焦距为 2c(c>0). 由题意得2a=10,2c=6,即a=5,c=3,
所以b2=a2-c2= 16,
所以椭圆C的方程为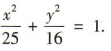 (2)设A(x1,y1),B(x2,y2).
由
(2)设A(x1,y1),B(x2,y2).
由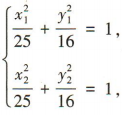 两式相减可得
两式相减可得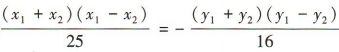 ,即
,即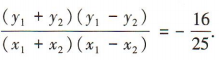 又点
又点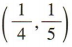 为线段 AB 的中点,
所以
为线段 AB 的中点,
所以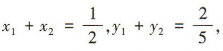 所以直线l的斜率
所以直线l的斜率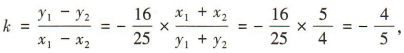 所以直线!的方程为
所以直线!的方程为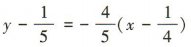 ,即4x+5y-2=0.
,即4x+5y-2=0.



