2025年高职单招《数学(中职)》每日一练试题09月04日

2025年高职单招《数学(中职)》每日一练试题09月04日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、角2023°的终边在()

• A：第一象限
• B：第二象限
• C：第三象限
• D：第四象限

答 案：C

解 析：易得2023°=5×360°+223°,223°的终边在第三象限，所以角2023°的终边在第三象限.

2、已知向量a=(1,-1),b=(2,x),若a·b=5,则x=()  

• A：-1
• B：3
• C：-3
• D：1

答 案：C

解 析：a·b=2-x=5,解得x=-3。

3、不等式lg(x-1)的定义域是( )  

• A：{x|x＜0}
• B：{x|x＞1}
• C：{x|x∈R}
• D：{x|0＜x＜1}

答 案：B

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、已知集合A={x|x<2a-1},B={x|x≥1},且A∪B=R,则实数a的取值范围是（）  

答 案：a≥1

解 析：由A∪B=R,A={x|x<2a-1},B={x|x≥1}得2a-1≥1,解得a≥1.

2、在等差数列{a_n}中,已知 a₅+a₈=5,则a₂+a₁₁=()  

答 案：5

解 析：由等差数列的性质可知a₂+a₁₁=a₅+a₈=5.

3、已知平面向量a=(-3,m),b=(m-2,-1),若a与b的方向相反，则实数m的值为（）  

答 案：3

解 析：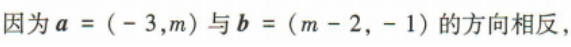

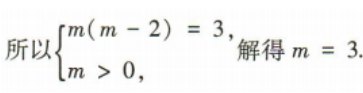
简答题

1、已知抛物线的顶点在原点,对称轴为y轴,焦点F(0,1).(1)求抛物线的标准方程;
(2)若过点A(0,m),且斜率为2的直线与该抛物线没有交点,求m的取值范围.  

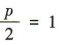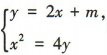答 案：(1)设抛物线的标准方程为x²=2py,P >0. 由题意可得,解得p= 2, 所以抛物线的标准方程为x²=4y. (2)设过点A(0,m),且斜率为2的直线的方程为y=2x+m. 由得x²-8x-4m=0. 因为直线与抛物线没有交点， 所以m=(-8)²-4(-4m)<0,解得m<-4. 所以m的取值范围是(-∞，-4).