2025年高职单招《数学(中职)》每日一练试题07月04日

2025年高职单招《数学(中职)》每日一练试题07月04日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知1g2=a,lg3=b,则lg12=()  

• A：
• B：a²b
• C：2a-b
• D：2a+b

答 案：D

解 析：lg12=1g(2²×3)=2lg2+lg3=2a+b.

2、经过两条直线2x+3y+1=0和x-3y+4=0的交点,并且垂直于直线3x+4y-7=0的直线的方程为（）

• A：3x-4y-9=0
• B：4x-3y-9=0
• C：3x-4y+9=0
• D：4x-3y+9=0

答 案：D

解 析：由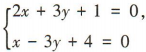得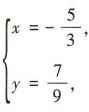,所以直线2x+3y+1=0和x-3y+4=0的交点坐标为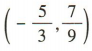,易知直线3x+4y-7=0的斜率为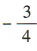,所以所求直线的斜率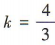,所以所求直线的方程为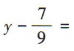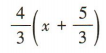,即4x-3y+9=0.

3、函数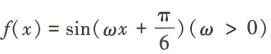的最小正周期为π,则=()  

• A：4
• B：2
• C：1
• D：

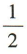
答 案：B

解 析：由函数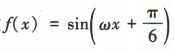的最小正周期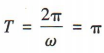,得=2.

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、函数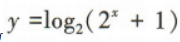的值域是（）  

答 案：(0,+∞)

解 析：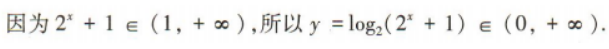

2、甲、乙两队进行篮球比赛,甲队获胜的概率为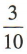,两队平局的概率为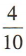,则甲队不输的概率是（）  

答 案：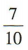

解 析：甲队不输即甲队获胜或两队平局,所以甲队不输的概率是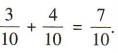

3、某同学6次技能测试的成绩分别是85,91,88,87,90,87,为了精确评价该同学技能发挥的稳定性,通过数据分析得到该组数据的标准差是()  

答 案：2

解 析：由题意知该组数据的平均数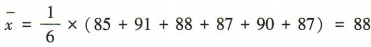,所以方差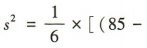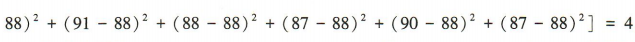，所以该组数据的标准差为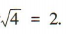

简答题

1、如图,在底面是矩形的四棱锥P-ABCD中,,E,F分别是 PC,PD的中点. (1)若PA=AB=1.BC=2.求四棱锥P-ABCD的体积; (2)证明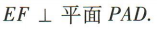  

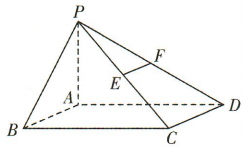
答 案：(1) ∴PA为四棱锥P-ABCD的高. 又PA=AB=1,BC=2,底面ABCD 是矩形， ∴ (2)∵四边形 ABCD 为矩形, ∴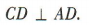 ∵ 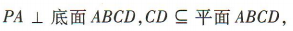∴ 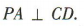又 ∴ 又E,F分别是 PC,PD的中点， ∴ EF // CD, ∴