2025年高职单招《数学(中职)》每日一练试题09月07日

2025年高职单招《数学(中职)》每日一练试题09月07日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知函数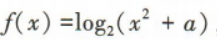,若f(3)=1,则a=（）

• A：7
• B：-7
• C：5
• D：-5

答 案：B

解 析：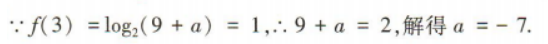

2、下列命题中正确的是（）

• A：第一象限角一定不是负角
• B：钝角一定是第二象限角
• C：小于90°的角一定是锐角
• D：第一象限角一定是锐角

答 案：B

解 析：令α=-300°=60°-360°,显然α是第一象限角，同时也是负角，但不是锐角，故A,D错误；不妨设θ是钝角，则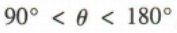,所以θ一定是第二象限角，故B正确；令β=-60°,显然β是小于90°的角，但不是锐角，故C错误.

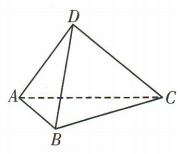
3、如图，在空间四边形ABCD中，AB=AD=AC=CB=CD=BD,则AC与BD所成的角为()  

• A：30°
• B：45°
• C：60°
• D：90° 解析：取AC的中点E,连接BE,D

答 案：D

解 析：取AC的中点E,连接BE,DE.因为AD=DC,AB=BC,E为AC的中点，所以AC⊥BE,AC⊥DE.又BE∩DE=E,DE,BE⊂平面BDE,所以AC⊥平面BDE.又BD⊂平面BDE,所以AC⊥BD,即AC与BD所成的角为90°.

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、正方体ABCD-A1B1C1D1中AC与AC1所成角的正弦值为=__________.  

答 案：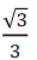

解 析：由于CC₁=1，AC₁=√3 ，所以角AC₁C的正弦值为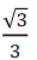

2、不等式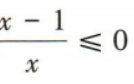的解集为（）

答 案：(0,1]

解 析：

3、函数y=|2x-1|的单调递增区间是（）  

答 案：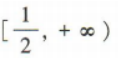

解 析：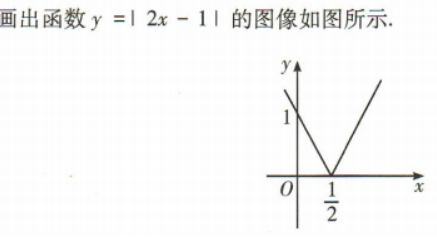

简答题

1、已知圆C:(x-2)²+(y-3)²= 4. (1)圆外有一点P(4,-1),过点P作直线l与圆C相切,求直线l的方程; (2)若直线x+y+m=0被圆C所截得的弦长为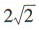,求m的值.  

答 案：(1)易知圆C:(x-2)²+(y-3)²= 4的圆心为(2,3),半径r= 2. 当直线l的斜率不存在时,直线l的方程为x=4,圆心到直线x=4的距离为2=r,符合题意. 当斜率存在时,设直线l的方程为kx-y-4k-1=0. 因为直线l与圆C相切， 所以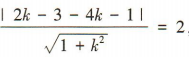,解得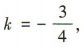 所以l的方程为3x+4y-8=0. 综上,直线l的方程为x=4或3x+4y-8=0. (2)易得圆心(2,3)到直线x+y+m=0的距离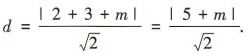 因为直线x+y+m=0被圆C所截得的弦长为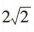, 所以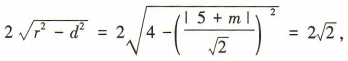 所以m=-3或m=-7.