2025年高职单招《数学(中职)》每日一练试题07月19日

2025年高职单招《数学(中职)》每日一练试题07月19日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知向量a,b满足|a|=1,|b|=2,a·(a+b)=0,则向量a与b的夹角为()

• A：
• B：
• C：
• D：

答 案：C

解 析：设向量a与b的夹角为θ.由a·(a+b)=0,得a²+|a||b|cosθ=0.又|a|=1,|b|=2,所以1+2cosθ=0，所以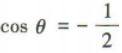。因为0＜θ＜π，所以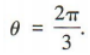

2、直线l:3x-y-6=0与圆C:x²+y²-2x-4y=0相交于A,B两点,则|AB|=()

• A：10
• B：5
• C：
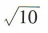
• D：

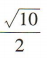
答 案：C

解 析：易知圆C:x²+y²-2x-4y=0即(x- 1)²+(y-2)²=5的圆心坐标为(1,2),半径为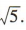因为点(1,2)到直线3x-y-6=0的距离为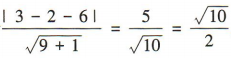,所以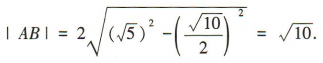

3、已知α是第三象限角，且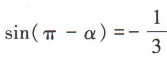,则cos(π+α)=（）  

• A：
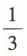
• B：
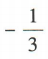
• C：
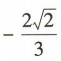
• D：

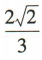
答 案：D

解 析：易知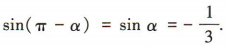因为α是第三象限角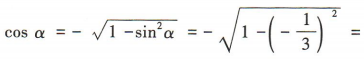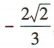，所以，所以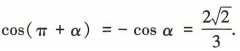

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、抛物线y²=4x的焦点到直线l:5x+12y+3=0的距离是()  

答 案：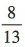

解 析：易知抛物线y²=4x的焦点坐标为(1,0),所以抛物线的焦点到直线l:5x+12y+3=0的距离d=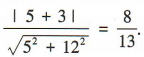

2、已知向量a=(4,3),b=(x,4),若a⊥b,则|b|=（）  

答 案：5

解 析：因为a⊥b,所以a·b=0.又a=(4,3),b=(x,4),所以4x+12=0,解得x=-3,所以b=(-3,4),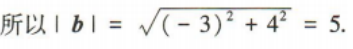

3、3(2a-b)-5(a+3b)=（）

答 案：a-18b

解 析：3(2a-b)-5(a+3b)=6a-3b-5a-15b=(6-5)a-(3+15)b=a-18b.

简答题

1、已知2＜a＜3,-2＜b＜3. (1)求3a+b的取值范围； (2)求a-b的取值范围.

答 案：(1)∵2＜a＜3, ∴6＜3a＜9, 又-2＜b＜3,∴4＜3a+b＜12. (2)∵-2＜b＜3,∴-3＜-b＜2, 又∵2＜a＜3,∴-1＜a-b＜5.