2025年成考专升本《高等数学一》每日一练试题07月20日
2025-07-20 11:19:55 来源：勒克斯教育网
2025年成考专升本《高等数学一》每日一练试题07月20日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、曲线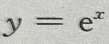
与其过原点的切线及y轴所围面积为（）
- A：
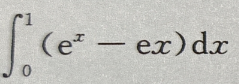
- B：
- C：
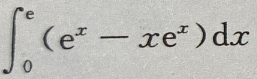
- D：
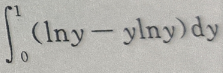
答 案：A
解 析：设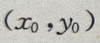
为切点，则切线方程为
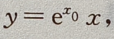联立
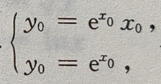得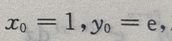
所以切线方程为y=ex，故所求面积为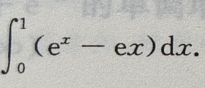
2、设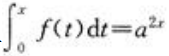
，其中f（x）为连续函数，a＞0且a≠1，则f（x）等于（）。
- A：2a2x
- B：a2x㏑a
- C：2xa2x-1
- D：2a2x㏑a
答 案：D
解 析：对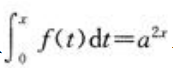
两边求导得：f（x）＝2a2xlna。
3、函数y＝f'（x）在点x0处可导是函数f（x）在点x0处连续的（）。
- A：充分条件
- B：必要条件
- C：充分必要条件
- D：既非充分也非必要条件
答 案：A
解 析：函数y＝f'（x）在点x0处可导，则必然在点x0处连续；但函数f（x）在点x0处连续，不一定得到函数在点x0处可导，所以函数y＝f'（x）在点x0处可导是函数f（x）在点x0处连续的充分非必要条件。
主观题
1、设函数，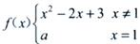
在x＝1处连续，求a。
答 案：解：f(x)在x＝1处连续，有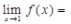
，
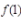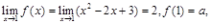
得a＝2。
2、设切线l是曲线y＝x2＋3在点（1，4）处的切线，求由该曲线，切线，及y轴围成的平面图形的面积S。
答 案：解：y＝x2＋3，＝2x。切点（1，4），y'（1）＝2．故切线l的方程为y－4＝2（x－1）,即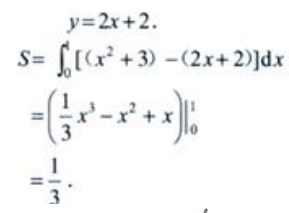
3、计算二重积分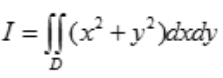
，其中D是x2＋y2≤1，x≥0，y≥0所围的平面区域．
答 案：解：D的图形见下图中阴影部分。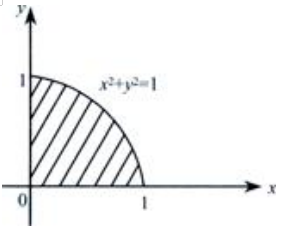
在极坐标系下D满足0≤
≤
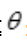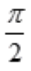，0≤r≤1，且x2＋y2＝（rcos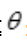）2＋（rsin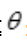）2＝r2，故
。
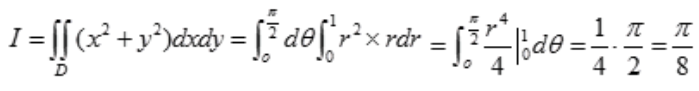填空题
1、设z=xtan(y2+1)，则
（）
答 案：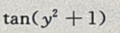
解 析：对x求偏导，可将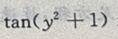
看作是常数，故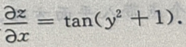
2、级数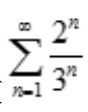
的和为（）。
答 案：2
解 析：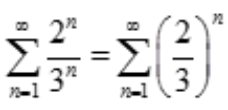
是首项为
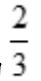，公比为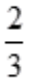
的几何级数，其和
。
3、设y＝x2ex，则y'＝（）。
答 案：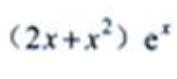
解 析：由函数乘积的导数公式，可得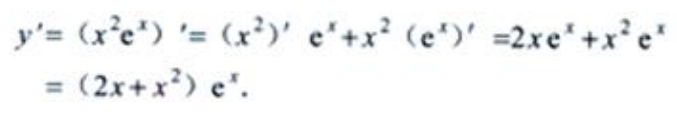
简答题
1、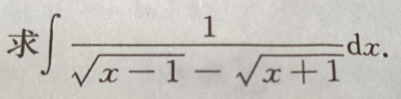
答 案：
- 备考交流
-
2025成考内部交流群群号：665429327
扫一扫或点击二维码入群
