2025年成考高起点《数学(文史)》每日一练试题10月10日

2025年成考高起点《数学(文史)》每日一练试题10月10日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

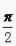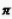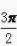1、cos+cos（-）+cot+sin+tan=（）。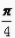

• A：2
• B：1
• C：-2
• D：-1

答 案：D

2、若|a|=1，|b|=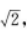（a-b）⊥a，则a与b的夹角为（　）

• A：30°
• B：45°
• C：60°
• D：75°

答 案：B

解 析：因为(a-b)⊥a， 【考点指要】本题考查向量的模与夹角的计算、向量的数量积的几何意义及对垂直问题的应用

3、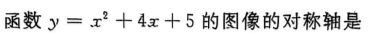

• A：
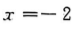
• B：
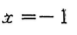
• C：
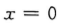
• D：

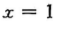
答 案：A

解 析：

4、过点A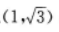与圆x²+y²=1相切的直线方程是（）

• A：
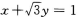
• B：
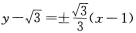
• C：
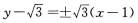
• D：以上都不是

答 案：D

解 析：【考点指要】本题主要考查的内容是利用点到直线的距离公式求直线的斜率，从而写出所求的直线方程，这是考试大纲要求掌握的概念．从近几年的试题分析可知，这类题的深度在今后成人高考中有可能加大，希望考生予以足够的重视．

主观题

1、已知三角形的三边边长组成公差为1的等差数列，且最大角是最小角的二倍，求三边之长。  

答 案：三角形的三边边长分别为4，5，6。

2、设全集U=R，集合A={x｜-5＜x＜5}，B={x｜0≤x≤7}，求CUA∩B．

答 案：解：全集U=R，A={x｜-5＜x＜5}，B=｛X｜0≤x≤7}，因为CuA={x｜x≤-5或x≥5}，所以CuA∩B={x｜x≤-5或x≥5}N{x｜0≤x≤7}={x｜5≤x≤7}，如图1—10所示。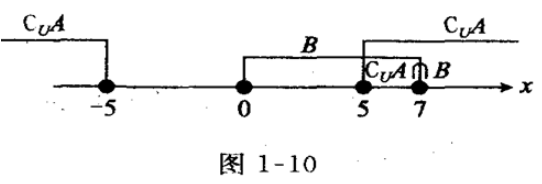

3、已知函数f（x）=（x-4）（x2-a）。（I）求f’（x）；
（Ⅱ）若f’（-1）=8，求f（x）在区间[0，4]的最大值与最小值。

答 案：(I)f'(x) =(x-4)'(x²-a)+(x-4)(x²-a)’ =x²-a+2x(x-4) =3x²-8x-a. (Ⅱ)由于f’(-1)=3+8-a=8,得a=3. 令f'(x)=3x²-8x-3=0,解得x1=3，（舍去）又f（0）=12，f（3）=-6，f（4）=0所以在区间[0，4]上函数最大值为12，最小值为-6

4、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。

答 案：(I)由题意,该抛物线的焦点到准线的距离为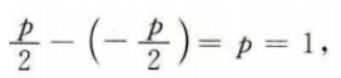 所以抛物线C的方程为y²=2x. (Ⅱ)因A(l,m)(m>0)为C上一点,故有m²=2, 可得 m=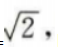因此A点坐标为 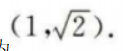设B点坐标为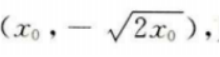

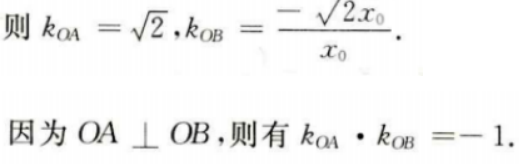
填空题

1、=______。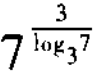

答 案：27

解 析：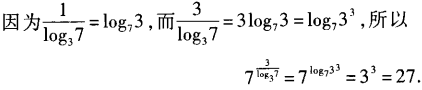

2、函数y=2cosx-cos2x（x∈R）的最大值为______。  

答 案：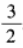

解 析：