2025年高职单招《数学》每日一练试题12月17日

2025年高职单招《数学》每日一练试题12月17日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、平面向量的加法运算遵循三角形法则。（）  

答 案：错

解 析：平面向量的加法运算遵循平行四边形法则和三角形法则。

2、在统计中，被抽取出来的个体的集合叫做样本容量。（）  

答 案：错

解 析：应该是样本。要考察的全体对象叫做总体。组成总体的每一个考察对象叫个体。抽样调查中，被抽取的那些个体叫样本。样本中个体的数目叫样本容量。

单选题

1、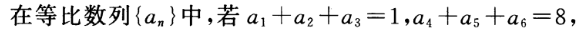则q等于（    ）

• A：-2
• B：2
• C：7/9
• D：-7/9

答 案：B

解 析：设等比数列{an}的公比为q， 由a₁+a₂+a₃=1  ①， a₄+a₅+a₆=q³（a1+a2+a3）=8  ②， ②÷①得：q³=8，∴q=2． 故选：B．

2、已知△ABC中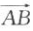，=a,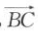=b,若a▪b>0,则该三角形是().  

• A：钝角三角形
• B：锐角三角形
• C：直角三角形
• D：等腰三角形

答 案：A

多选题

1、下列关系式正确的是（）  

• A：
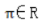
• B：-5∈Z
• C：
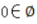
• D：1/2∈Q

答 案：ABD

解 析：A：R是实数，为有理数和无理数。B：在数学里用大写符号Z表示全体整数的集合，包括正整数、0、负整数。D：Q是有理数的集合。C：空集是没有任何元素的，因此也不会有元素0，因此C选项错误，ABD正确。

2、当函数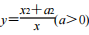在 x＝x₀处的导数为 0 时，那么 x₀可以是( )  

• A：a
• B：0
• C：-a
• D：a²

答 案：AC

解 析：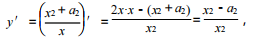

主观题

1、如图所示，在三棱锥P-ABC中，PB⊥平面ABC,AB⊥AC,垂足为点A (1)证明：AC⊥平面PAB; (2)若AC=3,BC=√10,直线PC与平面PAB所成的角为30°,求三棱锥B-PAC的体积.  

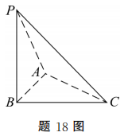
答 案：（1）证明：因为PB⊥平面ABC，AC⊆平面ABC，所以PB⊥AC 又因为AB⊥AC，AB,PB⊆平面PAB，AB∩PB=B, 所以AC⊥平面PAB （2）因为直线PC与平面PAB所成的角为30°，AC⊥平面PAB， 所以在直角三角形PAC中，∠CPA=30°,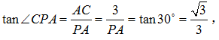 解得PA=3√3 又因为△ABC的面积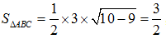，PB⊥平面ABC 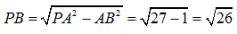所以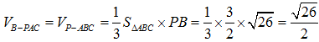  

2、已知抛物线C:x²=4y和直线7:2x+2y+m=0. (1)若抛物线C和直线l有两个交点，求m的取值范围； (2)若m＞1,且直线l与抛物线C有两个交点A,B,线段AB的垂直平分线交y轴于点P,求△PAB的面积S的取值范围。  

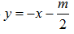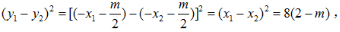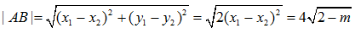答 案：（1）由2x+2y+m=0得 将其代入x²=4y中得x²+4x+2m=0， 所以△=4²-4×1×2m=16-8m. 因为抛物线C和直线l有两个交点，所以△=16-8m＞0，解得m＜2. 因此，m的取值范围是（-∞，2） （2）设点A（x₁，,y₁），B（x₂，y₂），则由方程x²+4x+2m=0可得x₁+x₂=-4，x₁x₂=2m， （x₁-x₂)²=（x₁+x₂)²-4x₁x₂=8（2-m）; 所以 因为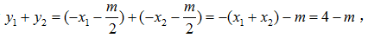 所以线段AB的中点 k_AB=-1， 所以过点Q与线段AB垂直的直线方程为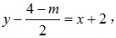 即2x-2y+8-m=0. 该直线与y轴的交点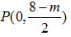到直线l的距离 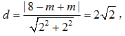所以△PAB的面积 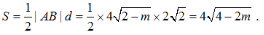因为1＜m＜2，所以0＜4-2m＜2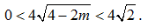， 因此，△PAB的面积S的取值范围是（0，4√2）  

填空题

1、请观察数列：1，1，2，3，5，（　　），13…运用合情推理，括号里的数最可能是（　　）  

答 案：8

解 析：由已知可得：该数列从第三项开始，每一项等于前两项的和， 由3+5=8得，括号里的数最可能的是8  

2、集合{x，x²+2x-6}中实数x所满足的条件是_____

答 案：x≠-3 且 x≠2

解 析： 故答案为：x≠-3 且 x≠2