2025年高职单招《数学》每日一练试题11月30日

2025年高职单招《数学》每日一练试题11月30日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、函数f（x）=（x-1）（x²+3x-10）有3个零点。（）  

答 案：对

2、各边相等的多边形是正多边形。（）  

答 案：错

解 析：菱形的各边相等，但它不一定是正方形。

单选题

1、一组对边平行，并且对角线互相垂直且相等的四边形是（）  

• A：菱形或矩形
• B：正方形或等腰梯形
• C：矩形或等腰梯形
• D：菱形或直角梯形

答 案：B

解 析：根据菱形、矩形、正方形等的判定可知:正方形或等腰梯形的一组对边平行，对角线相等且可以互相垂直.此题主要考查了正方形的判定，学生对这些概念类的知识一定要牢固掌握．这是数学中的基础.

2、等差数列{a_n}的前n项和为S_n，若a₃=4，S₉=18，则公差d=（）  

• A：1
• B：-1
• C：2
• D：-2

答 案：B

多选题

1、下列命题中，不正确的是（）  

• A：三点可确定一个圆
• B：三角形的外心是三角形三边中线的交点
• C：一个三角形有且只有一个外接圆
• D：三角形的外心必在三角形的内部或外部

答 案：ABD

解 析：A、不在同一条直线上的三点确定一个圆，故本选项错误；B.、三角形的外心是三角形三边垂直平分线的交点，所以本选项是错误；C、三角形的外接圆是三条垂直平分线的交点，有且只有一个交点，所以任意三角形一定有一个外接圆，并且只有一个外接圆，所以本选项是正确的；D、直角三角形的外心在斜边中点处，故本选项错误。故选：ABD

2、已知函数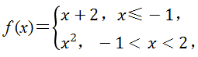关于函数f(x)的结论正确的是(　　)  

• A：f(x)的值域为(－∞，4)
• B：f(1)＝3
• C：若f(x)＝3，则x的值是
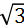
• D：f(x)<1的解集为(－1，1)

答 案：AC

解 析：当x≤－1时，f(x)的取值范围是(－∞，1]，当－1＜x＜2时，f(x)的取值范围是[0，4)，因此f(x)的值域为(－∞，4)，故A正确；当x＝1时，f(1)＝12＝1，故B错误；当x≤－1时，由x＋2＝3，解得x＝1(舍去)，当－1＜x＜2时，由x2＝3，解得x＝或x＝－(舍去)，故C正确；当x≤－1时，由x＋2＜1，解得x＜－1，当－1＜x＜2时，由x²＜1，解得－1＜x＜1，因此f(x)＜1的解集为(－∞，－1)∪(－1，1)，故D错误.故选AC.

主观题

1、对于三次函数f（x）=ax³+bx²+cx+d（a≠0），定义：f"（x）是函数y=f（x）的导数f’(x)的导数，若方程f"(x)=0有实数解x₀，则称点(x₀，f（x₀））为函数y=f（x）的“拐点”有同学发现“任何一个三次函数都有‘拐点”；任何一个三次函数都有对称中心，且‘拐点’就是对称中心”已知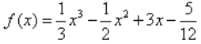， (1)分别求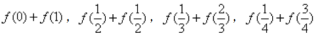的值，然后归纳猜想一般性结论并证明； (2)求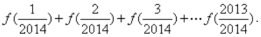

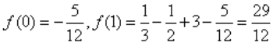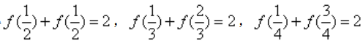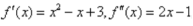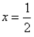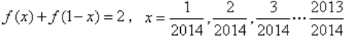答 案：解：（1）通过计算所以f(0)+f(1)=2， 同理可得， 由此猜想f(x)+f(1-x)=2. 因为由2x-1=0得， 因为， 所以f(x)的对称中心为. 所以f(x)+f(1-x)=2. (2)由（1）知，， 所以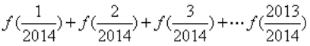 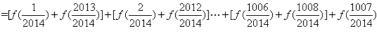=2×2016+1 =2013.

2、为迎接党的“十九大”胜利召开与响应国家交给的“提速降费”任务，某市移动公司欲提供新的资费套餐（资费包含手机月租费、手机拨打电话费与家庭宽带上网费）。其中一组套餐变更如下： 原方案资费 新方案资费 （1）客户甲（只有一个手机号和一个家庭宽带上网号）欲从原方案改成新方案，设其每月手机通话时间为x分钟（x∈N^*），费用原方案每月资费-新方案每月资费，写出y关于x的函数关系式； （2）经过统计，移动公司发现，选这组套餐的客户平均月通话时间x≤400分钟，为能起到降费作用，求的取值范围。

答 案：（1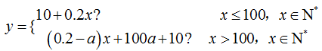） （2）0.2＜a＜0.3

解 析：（1）i)x≤100，y=68+0.2x-58=10+0.2x ii)当x＞100，y=68+0.2x-[58+(x-100)a]=（0.2-a）x+100a+10 综上所述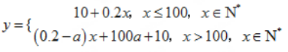 （2）由题意，x≤400,y＞0恒成立， 显然，当x≤100，x∈N^*，y＞0 当100＜x≤400，因为0.2-a＜0， y=(0.2-a)x+100a+10为减函数 所以当y=400时，y_min=90-300a＞0 解得a＜0.3 从而0.2＜a＜0.3

填空题

1、在等比数列中，a₂=3，q=2，则a₅=______  

答 案：24

2、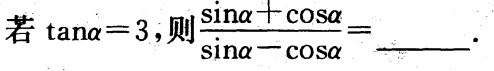  

答 案：2