2025年高职单招《数学(中职)》每日一练试题11月14日

2025年高职单招《数学(中职)》每日一练试题11月14日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知扇形的周长为6cm,半径是2cm,则该扇形圆心角的弧度数是（）

• A：1
• B：2
• C：3

答 案：A

解 析：

2、若函数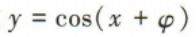的一个零点是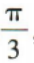则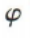可以取的值是（）

• A：
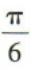
• B：
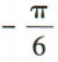
• C：
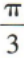
• D：

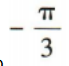
答 案：A

解 析：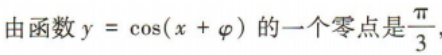

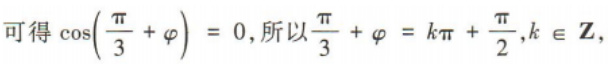
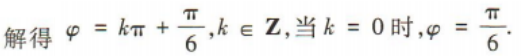
3、函数f(x)=-x²+1在区间[-1,2]上的最小值为

• A：0
• B：1
• C：-3
• D：-5

答 案：C

解 析：易知f(x)=-x²+1的图像开口向下，其对称轴为y轴，所以f(x)在区间[-1,2]上的最小值为f(2)=-3.

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、设△ABC的内角A,B,C的对边分别为a,b,c,已知4a=3b,B=2A,则cosA=（）  

答 案：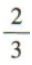

解 析：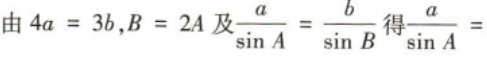

2、若椭圆上一点到两焦点F₁(-2,0),F₂(2,0)的距离之和为8,则该椭圆的短轴长为()  

答 案：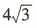

解 析：由题知c= 2,2a=8,即a=4,故b²=a²-c²=12,得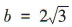,所以该椭圆的短轴长为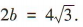

3、若(x-1)ⁿ的展开式中x²的系数是-10,则n的值为()  

答 案：5

解 析：因为(x-1)ⁿ的展开式中x²的系数是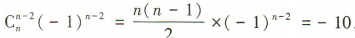,所以n= 5.

简答题

1、某医院有内科医生8名,外科医生6名,现从中选派4人参加抗灾救援医疗队,分别求符合下列条件的选法种数.(1)甲、乙两人至少有一人参加;
(2)队中至少有一名内科医生和一名外科医生.  

答 案：(1)从 14名医生中选派4人,所有可能的情况有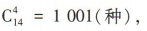 其中甲、乙两人都没被选派的情况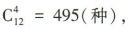有 故甲、乙两人至少有一人参加的情况有1001-495 =506(种). (2)此时4名医生组成的医疗队有如下三种情况: ①1名内科医生,3名外科医生,选法共有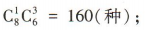 ②2名内科医生,2名外科医生,选法共有 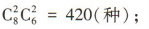③3名内科医生,1名外科医生,选法共有 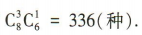因此队中至少有一名内科医生和一名外科医生的情况共有160+420+336=916(种).