2025年高职单招《数学》每日一练试题10月23日

2025年高职单招《数学》每日一练试题10月23日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、抛物线y=x²的顶点是原点。（）  

答 案：对

解 析：顶点式：y=a(x-h)^2+k抛物线的顶点P（h,k）,则为p（0,0）

2、甲、乙两台机床，它们因故障停机的概率分别为0.01和0.02，则这两台机床同时因故障停机的概率为0.03。（）  

答 案：错

单选题

1、已知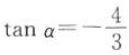,则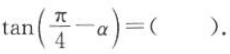

• A：-7
• B：7
• C：
• D：

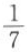
答 案：A

解 析：故选A.

2、空间中，垂直于同一直线的两条直线（）  

• A：平行
• B：相交
• C：异面
• D：以上均有可能

答 案：D

解 析：两直线的位置关系有三种:平行，相交，异面，判定时常借助于长方体分析，本题中选D

多选题

1、已知等差数列{a_n}的前n项和为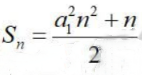，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：2S_n-a_n=1+3+5+...+(2n-1)
• D：

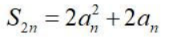
答 案：ABC

2、已知数列{3n-1}，下面选项正确的是（）  

• A：这个数列是公比为3的等比数列
• B：这个数列是公差为3的等差数列
• C：这个数列的第5项是14
• D：20是这个数列的第7项

答 案：BCD

解 析：已知数列{3n-1}，这个数列是公差为3的等差数列，故A错误，B正确。数列第五项=3*5-1=14。故C正确。数列第七项=3*7-1=20.故D正确

主观题

1、甲、乙两支球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束.除第五局甲队获胜的概率是外，其余每局比赛甲队获胜的概率都是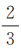.假设各局比赛结果相互独立. (1)分别求甲队以3:0,3:1,3:2获得比赛胜利的概率； (2)若比赛结果为3:0或3:1,则胜利方得3分，对方得0分；若比赛结果为3:2,则胜利方得2分，对方得1分.求乙队得分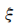的分布列和数学期望.  

答 案：（1）设“甲队以3:0胜利”为事件A，“甲队以3:1胜利”为事件B，“甲队以3:2胜利”为事件C，则 （2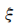）的所有可能取值为0,1,2,3,设“乙队以3:2胜利”为事件D，由于各局比赛结果相互独立， 则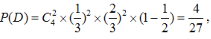 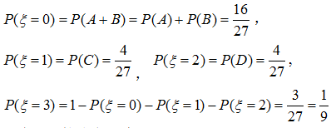因此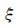，的分布列为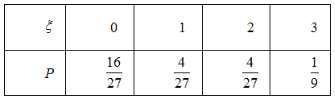 的数学期望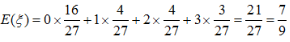  

2、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

填空题

1、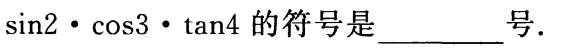  

答 案：负

2、已知函数f(x)=lg x,则f(100)-f(1)=（）.

答 案：2

解 析：因为f(x)=lg x,所以f(100)-f(1)=lg 100-lg 1=2-0=2.