2025年高职单招《数学》每日一练试题09月21日

2025年高职单招《数学》每日一练试题09月21日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、设π/4＜a＜π，则有sina＞cosa。（）  

答 案：对

解 析：一全正，二正弦，三正切，四余弦（口诀）但是在第一象限以π/4发现为基准，当a大于π/4时，sina＞cosa，当a小于π/4时，sina＜cosa，第二象限中sina是正，cosa是余弦是负数，所以π/4＜a＜π，则有sina＞cosa，是正确的。

2、各个角相等的圆内接多边形是正多边形。（）  

答 案：错

解 析：圆内接矩形的各角都相等，但它不一定是正方形。

单选题

1、抛物线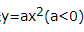的焦点坐标为(          ). 

• A：
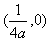
• B：
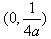
• C：
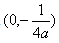
• D：

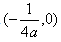
答 案：B

解 析：

2、一组对边平行，并且对角线互相垂直且相等的四边形是（）  

• A：菱形或矩形
• B：正方形或等腰梯形
• C：矩形或等腰梯形
• D：菱形或直角梯形

答 案：B

解 析：根据菱形、矩形、正方形等的判定可知:正方形或等腰梯形的一组对边平行，对角线相等且可以互相垂直.此题主要考查了正方形的判定，学生对这些概念类的知识一定要牢固掌握．这是数学中的基础.

多选题

1、下列命题中正确的个数是(　　)  

• A：若a，b，c成等差数列，则a2，b2，c2一定成等差数列；
• B：若a，b，c成等差数列，则2a,2b,2c可能成等差数列；
• C：若a，b，c成等差数列，则ka＋2，kb＋2，kc＋2一定成等差数列；
• D：若a，b，c成等差数列，则1/a，1/b，1/c可能成等差数列．

答 案：BCD

解 析：对于A取a＝1，b＝2，c＝3,a2＝1，b2＝4，c2＝9，A错； 对于B，a＝b＝c，2a＝2b＝2c，B正确；对于C，∵a，b，c成等差数列，∴a＋c＝2b.∴(ka＋2)＋(kc＋2)＝k(a＋c)＋4＝2(kb＋2)，C正确；对于D，a＝b＝c≠0?1/a=1/b=1/c，D正确。综上可知选BCD。  

2、下列关系式正确的是（）  

• A：
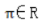
• B：-5∈Z
• C：
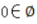
• D：1/2∈Q

答 案：ABD

解 析：A：R是实数，为有理数和无理数。B：在数学里用大写符号Z表示全体整数的集合，包括正整数、0、负整数。D：Q是有理数的集合。C：空集是没有任何元素的，因此也不会有元素0，因此C选项错误，ABD正确。

主观题

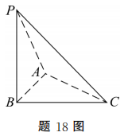
1、如图所示，在三棱锥P-ABC中，PB⊥平面ABC,AB⊥AC,垂足为点A (1)证明：AC⊥平面PAB; (2)若AC=3,BC=√10,直线PC与平面PAB所成的角为30°,求三棱锥B-PAC的体积.  

答 案：（1）证明：因为PB⊥平面ABC，AC⊆平面ABC，所以PB⊥AC 又因为AB⊥AC，AB,PB⊆平面PAB，AB∩PB=B, 所以AC⊥平面PAB （2）因为直线PC与平面PAB所成的角为30°，AC⊥平面PAB， 所以在直角三角形PAC中，∠CPA=30°,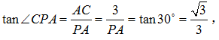 解得PA=3√3 又因为△ABC的面积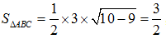，PB⊥平面ABC 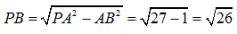所以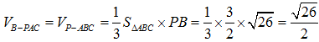  

2、在等差数列{a_n}中，a₅=-10,a₁₀=0. (1)求数列{a_n}的通项公式； (2)记数列{a_n}的前n项和为S_n,当n为何值时，S_n有最小值?最小值是多少?  

答 案：（1）设等差数列{a_n}的公差为d， 则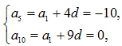解得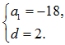 因此，数列{a_n}的通项公式为a_n=-18+2(n-1)，即a_n=2n-20 （2）由等差数列的前n项和公式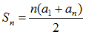得 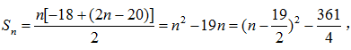所以当n=9或n=10时，S_n有最小值-90  

填空题

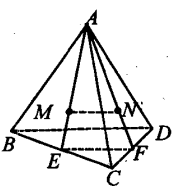
1、如图，A是∆BCD所在平面外一点，M,N分别是∆ABC和∆ACD的重心，若BD=a，则MN=_______.

答 案：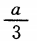

解 析：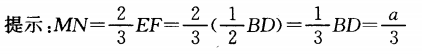

2、在四边形ABCD中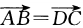， ，且 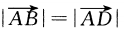，则四边形ABCD是___形.  

答 案：菱形