2025年高职单招《数学(中职)》每日一练试题05月10日

2025年高职单招《数学(中职)》每日一练试题05月10日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

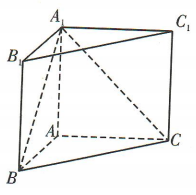
1、如图，在三棱柱ABC-A₁B₁C₁中，A₁A⊥底面ABC,AB⊥AC,A₁A=AB=AC=2,那么三棱锥A₁-ABC的体积是（）  

• A：
• B：
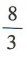
• C：4
• D：8

答 案：A

解 析：易知A₁A为三棱锥A₁-ABC的高.由AB⊥AC，A₁A=AB=AC=2，得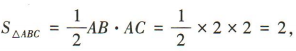

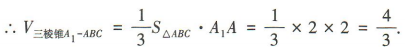
2、如图，在三棱锥A-BCD中，E,F分别是AB,AD的中点，则下列结论正确的是()  

• A：EF⊥平面BCD
• B：EF//平面BCD
• C：EF//平面ACD
• D：EFC平面BCD

答 案：B

解 析：因为E,F分别是AB,AD的中点，所以EF//BD.又EF⊄平面BCD,BD⊂平面BCD,所以EF//平面BCD

3、已知两个非零向量a和b满足a·b=0,则a与b的夹角为()

• A：180°
• B：90°
• C：45°
• D：0°

答 案：B

解 析：设向量a,b的夹角为α,α∈[0°,180°].因为向量a,b是非零向量，所以|a|≠0,|b|≠0.由a·b=|a|·|b|cosα=0可得cosα=0,故α=90°,即向量a,b的夹角为90°.

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、设ω为实数，函数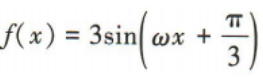的最小正周期为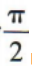则ω的值为（）

答 案：±4

解 析：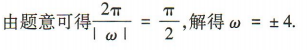

2、满足M∪{1}={0.1.2}的集合M的个数为()  

答 案：2

解 析：因为M∪{1}={0,1,2},所以0,2必须是集合M中的元素，1可以是集合M中的元素，也可以不是集合M中的元素，所以M={0,2}或M={0,1,2},所以满足题意的M的个数是2.

3、某大学的两名教授带领四名学生外出实习,实习前在学院门口合影留念,若站成两排合影,两名教授站在前排,四名学生站在后排,则不同的排法种数为（）  

答 案：48

解 析：先排两名教授,则不同的排法有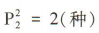;再排四名学生,则不同的排法有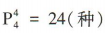.故不同的排法有2x24 =48(种).

简答题

1、平行四边形ABCD中，BD=2√3,AB=2,AD=4,将△CBD沿对角线BD折到△EBD,使得平面CBD丄平面ABD，求证：AB丄DE.  

答 案：证明: 在△ABD中，AB=2,AD=4,BD=2√3 则AB²+BD²=AD²，故AB⊥BD， 又平面EBD⊥平面ABD，交线为BD，而AB⊥BD 故AB⊥平面EBD, 则AB⊥DE.