2025年成考高起点《数学(文史)》每日一练试题11月20日

2025年成考高起点《数学(文史)》每日一练试题11月20日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若集合M={（x，y）｜3x-2y=-1}，N={（x，y）｜2x+3y=8}，则M∩N=（）。  

• A：（1，2）
• B：{1，2}
• C：{（1，2）}
• D：φ

答 案：C

解 析：M，N都是点集，所以只能选C。  

2、与圆x²+y²=4关于点M(3，2)成中心对称的曲线方程是（　）  

• A：
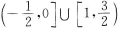
• B：
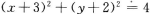
• C：
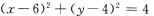
• D：

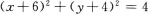
答 案：C

解 析：与圆关于点M成中心对称的曲线还是圆．只要求出圆心和半径，即可求出圆的方程．圆x²+y²=4的圆心(0，0)关于点M(3，2)成中心对称的点为(6，4)，所以所求圆的圆心为(6，4)，半径与对称圆的半径相等，所以所求圆的方程为(x-6)²+(y-4)²=4． 【考点指要】本题主要考查中心对称图形的定义、中点坐标公式的灵活运用、圆的标准方程的求法，这些主要概念在考试大纲中要求掌握，同时也是近几年经常考到的知识点．

3、由数字1、2、3、4组成没有重复数字的两位数共有（）。

• A：6个
• B：12个
• C：8个
• D：10个

答 案：B

4、直线绕原点按逆时针方向旋转30°后所得直线与圆（x-2）²+y²=3的位置关系是（）。

• A：直线过圆心
• B：直线与圆相交，但不过圆心
• C：直线与圆相切
• D：直线与圆相离

答 案：C

主观题

1、设函数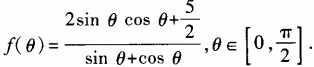 （1）求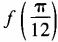；（2）求函数f（θ）最小值。

答 案：

2、教室里有50人在开会，其中学生35人，家长12人，老师3人，现校长在门外听到有人在发言，那么发言人是老师或学生的概率为多少？  

答 案：此题属于互斥事件，发言人是老师的概率为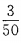，是学生的概率为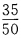，故所求概率为。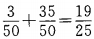

3、已知三角形的三边边长组成公差为1的等差数列，且最大角是最小角的二倍，求三边之长。  

答 案：三角形的三边边长分别为4，5，6。

4、设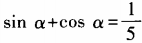（0＜α＜π），求tanα的值。  

答 案：

填空题

1、已知tanα=2，则=______。  

答 案：

2、“x²=4”是“x=2”的______。  

答 案：必要不充分条件