2025年成考高起点《数学(文史)》每日一练试题10月05日

2025年成考高起点《数学(文史)》每日一练试题10月05日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、函数f(x)=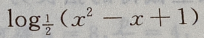的单调增区间是（）

• A：
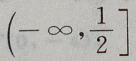
• B：
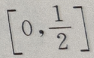
• C：
• D：

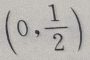
答 案：A

解 析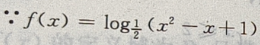：中的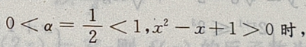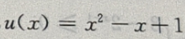的减区间就为f(x)的增区间，设u(x)=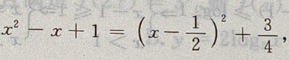当x∈R时，u(x)>0,函数u(x)在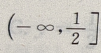是减函数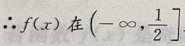， 上是增函数 故f(x)=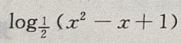的单调增区间为 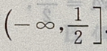ps：关于复合函数的问题要逐步分清每一层次的函数的图像和性质,再结合起来考虑整体,有时也可画出部分函数的图像来帮助分析和理解.  

2、甲坛有8个小球，乙坛有4个小球，所有小球颜色各不相同，现从甲坛中取2个小球，乙坛中取1个小球，则取出3个球的不同取法共有（）。

• A：224种
• B：112种
• C：32种
• D：1320种

答 案：B

解 析：C8（2）×C4（1）=112（种）。  

3、已知函数f(x)的定义域为R，且满足f(2x)=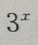,则f(x)的反函数为（）

• A：
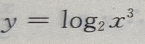
• B：
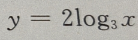
• C：
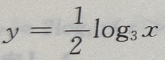
• D：

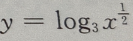
答 案：B

解 析：令2x=t，则x=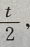  

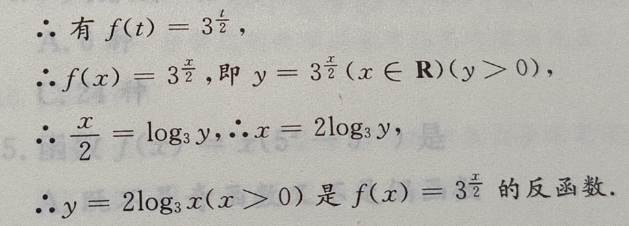
4、若角α终边上有一点P（3a，-4a），a＜0，则sinα·tanα的值是（）。

• A：
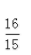
• B：
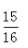
• C：
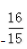
• D：

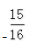
答 案：C

主观题

1、求证：双曲线的一个焦点到一条渐近线的距离等于虚半轴的长．  

答 案：设双曲线的方程为 则它的焦点坐标为F1(-c,0),F2(c,0),其中c²=a²+b²,渐近线方程为 令设焦点F2(c,0)到渐近线 的距离为d,则 即从双曲线的一个焦点F2(c,0)到一条渐近线的距离等于虚半 轴的长b，由上述推导过程可知，点F2到渐近线以及点F1(-c,0)到渐近线 的距离都等。 由于证明中只涉及a，b，c，而与双曲线的位置无关，所以这个结论对于任意双曲线都成立．

解 析：本题考查的是圆锥曲线与直线位置关系的推理能力，主要是用代数的方法表示几何中的问题．考生必须对曲线方程、几何性质及元素之间的关系有深刻的理解，方可解决此类综合题．这种综合性的圆锥曲线试题出现的概率比较高，要引起重视．

2、在△ABC中，B=120°,C=30°,BC=4，求△ABC的面积．

答 案：因为A= 180°-B-C=30°，所以AB = BC=4.因此△ABC的面积

3、求函数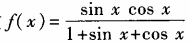（x∈R）的最大值与最小值。  

答 案：设sinx+cosx=t，则（sinx+cosx）²=t²，1+2sinxcosx=t²，sinxcosx= 于是转化为求的最值。 由所设知 上为增函数，故g（t）的最大值为最小值为

4、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。

答 案：(I)由题意,该抛物线的焦点到准线的距离为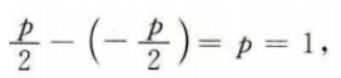 所以抛物线C的方程为y²=2x. (Ⅱ)因A(l,m)(m>0)为C上一点,故有m²=2, 可得 m=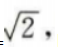因此A点坐标为 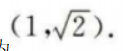设B点坐标为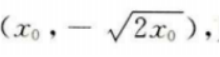

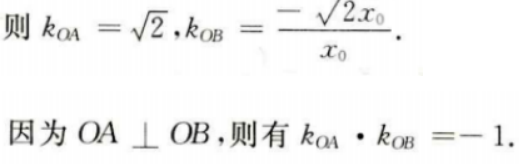
填空题

1、甲、乙、丙三位教师担任6个班的课，如果每人任选两个班上课有______种不同的任课方法。  

答 案：90

2、已知关于t的二次方程t²-6tsinθ+tanθ=0（0＜θ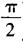＜）的两根相等，则sinθ+cosθ的值等于______。  

答 案：

解 析：