2025年成考高起点《数学(理)》每日一练试题07月18日
2025-07-18 12:15:29 来源:勒克斯教育网
2025年成考高起点《数学(理)》每日一练试题07月18日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设甲:二次不等式x2+px+q>0的解集为空集合;乙:△=p2-4q<0则()。
- A:甲是乙的必要条件,但不是乙的充分条件
- B:甲是乙的充分条件,但不是乙的必要条件
- C:甲不是乙的充分条件,也不是乙的必要条件
- D:甲是乙的充分必要条件
答 案:D
解 析:由于二次不等式x2+px+q>0的解集为空集合△=p2-4q<0,则甲是乙的充分必要条件(答案为 D)
2、设F1,F2分别是椭圆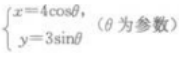 焦点,并且B1是该椭圆短轴的一个端点,则△F1F2B1的面积等于()。
焦点,并且B1是该椭圆短轴的一个端点,则△F1F2B1的面积等于()。
- A:
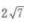
- B:
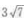
- C:
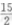
- D:2
答 案:B
解 析:消去参数,将参数方程化为普通方程,F1F2分别是椭圆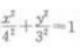 的焦点。
的焦点。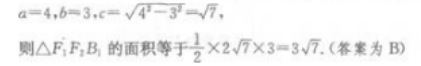
3、
- A:
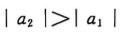
- B:
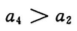
- C:
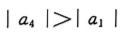
- D:
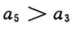
答 案:D
解 析: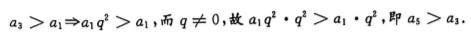
4、过A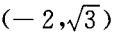 B(-5,0)两点直线的倾斜角为()。
B(-5,0)两点直线的倾斜角为()。
- A:
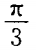
- B:
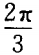
- C:
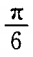
- D:
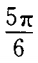
答 案:C
解 析: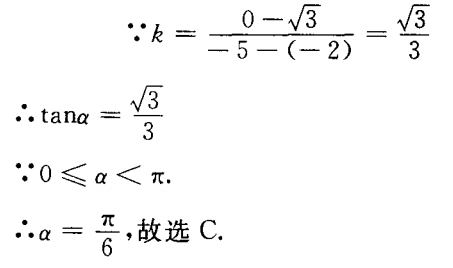
主观题
1、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35°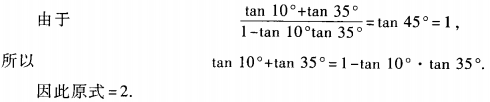
2、已知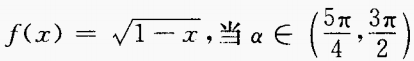 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得, 3、在△ABC中如果sinA=2sinBcosC,求证:△ABC是等腰三角形。
答 案: 4、已知am= 答 案: 填空题 1、在自然数1、2、…、100中任取一个数,该数能被3整除的概率是______。
答 案:0.33 解 析:此题随机试验包含的基本事件总数n=100,且每个数能被取到的机会均等,即属于等可能事件的概率能被3整除的自然数的个数m=33,故所求概率 2、100件产品中有3件次品,每次抽取一件,有放回的抽取三次,恰有1件是次品的概率是______。
答 案:0.0847 解 析:由于三次抽取是独立的,每次抽取可看做是一次试验,每次试验只有两个可能结果:“正品”或“次品”,次品率为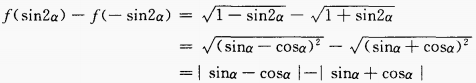
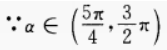 ∴sinα
∴sinα ∴△ABC为等腰三角形。
∴△ABC为等腰三角形。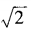 ,an=
,an=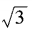 ,求a3n-4m的值。
,求a3n-4m的值。
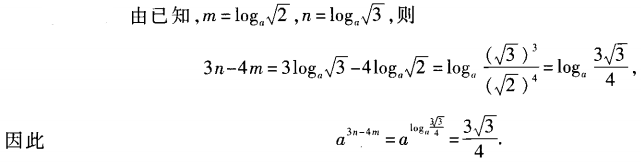
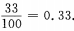
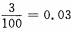 ,因此二次独立且重复试验恰有1件次品率为
,因此二次独立且重复试验恰有1件次品率为