2025年高职单招《数学(中职)》每日一练试题10月21日

2025年高职单招《数学(中职)》每日一练试题10月21日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若a＜b,则下列结论不一定成立的是()

• A：
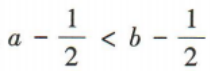
• B：2a＜2b
• C：
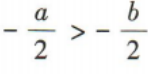
• D：a²＜b²

答 案：D

解 析：∵a＜b,∴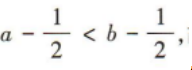 故A不符合题意；∵a＜b,∴:2a＜2b,故B不符合题意；∵a＜b, 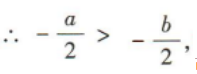故C不符合题意；当a=-2,b=0时，满足a＜b,但(-2)²＞0²,不满足a²＜b²,故D符合题意.

2、某高校有4名志愿者参加社区志愿工作,若每天有早、中、晚三班,每班1人,每人每天最多值一班,则值班当天不同的排班种数为（）

• A：12
• B：18
• C：24
• D：144

答 案：C

解 析：由题意知,4名志愿者参加社区志愿工作,每天早、中、晚三班,每班1人,每人每天最多值一班, ∴值班当天不同的排班种数为

3、对于复数z=3+2i说法错误的是（  ）.  

• A：它在复平面上对应点（3,2）
• B：虚部为2
• C：实部为3
• D：它的共轭复数为-3-2i

答 案：D

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、若则cos(π-α)=（）

答 案：

解 析：

2、已知α是第二象限角，若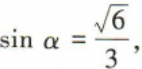tanα=（）

答 案：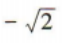

解 析：  

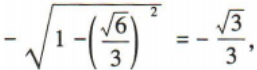
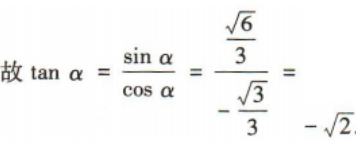
3、袋中装有大小、形状完全相同的6个白球,4个红球,从中任取一球,则取到白球的概率为（）  

答 案：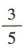

解 析：因为一共有 10 个球,所以从中任取一球的基本事件有 10个,又有6个白球,所以取到白球的基本事件有6个,所以取到白球的概率为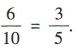

简答题

1、如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,点M,Q分别是PA,PD的中点,AC与BD交于点 N. 证明:(1)MN//平面PCD;
(2)平面MNQ//平面PBC.  

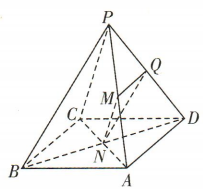
答 案：(1)∵四棱锥 P-ABCD 的底面 ABCD 为平行四边形, ∴N是 AC的中点. 又点M是PA的中点: ∴MN//PC. ∵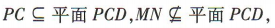 ∴MN//平面PCD. (2)由(1)知MN//PC,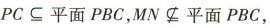 ∴MN//平面PBC. 又Q是PD的中点,N是BD的中点, ∴NQ// PB. ∴NQ//平面PBC. 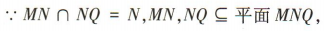∴平面MNQ/平面PBC.