2025年高职单招《数学(中职)》每日一练试题08月21日
2025-08-21 16:10:33 来源:勒克斯教育网
2025年高职单招《数学(中职)》每日一练试题08月21日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、sin150°=()
- A:
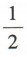
- B:
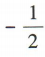
- C:
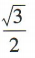
- D:
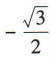
答 案:A
解 析: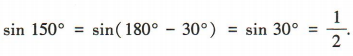
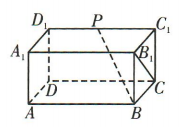
2、如图,在长方体ABCD-A₁B₁C₁D₁中,BB₁=BC,P为C₁D₁的中点,则异面直线PB与B₁C所成角的大小为()
- A:30°
- B:45°
- C:60°
- D:90°
答 案:D
解 析:连接BC1,AD1.在长方体ABCD-A1B1C1D1中,由BB1=BC得侧面BCC1B1是正方形,所以BC1⊥B1C.由D1C1⊥平面BCC1B1,B1C⊂平面BCC1B1,得D1C1⊥B1C.又D1C1∩BC1=C1,D1C1⊂平面ABC1D1,BC1⊂平面ABC1D1,所以B1C1⊥平面ABC1D1,又BP⊂平面ABC1D1,所以B1C⊥BP,即异面直线PB与B1C所成角的大小为90°。
3、如图,正方体ABCD-A₁B₁C₁D₁的棱长为4,S为A₁C₁与B₁D₁的交点,则四棱锥S-ABCD的体积为() 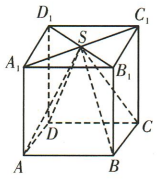
- A:
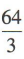
- B:
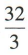
- C:
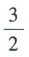
- D:2
答 案:A
解 析:由题意得四棱锥S-ABCD的高为4,则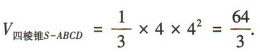
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、已知方程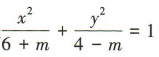 表示焦点在y轴上的椭圆,则实数m的取值范围是()
表示焦点在y轴上的椭圆,则实数m的取值范围是()
答 案:(-6,-1)
解 析:因为方程 2、已知 a1 ,a2的平均数为 6.5,且 a3,a4,a5的平均数为9,则 a1 ,a2,a3,a4,a5的平均数为()
答 案:8 解 析:因为a1 ,a2的平均数为6.5,所以 a1+a2= 13. 因为a3,a4,a5的平均数为9,所以a3+a4+a5= 27,所以a1,a2,a3,a4,a5的平均数为 3、已知tanα=2 答 案: 解 析: 简答题 1、制作一个高为20cm的长方体容器,底面矩形的长比宽长10cm,并且容积不少于4000cm3,问底面矩形的宽至少应是多少? 答 案:设底面矩形的宽为x cm. 由题意可得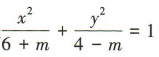 表示焦点在y轴上的椭圆,所以
表示焦点在y轴上的椭圆,所以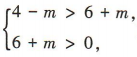 解得 -6
解得 -6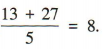
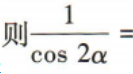 ()
()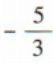
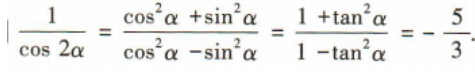

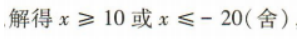 所以底面矩形的宽至少为10cm.
所以底面矩形的宽至少为10cm.



