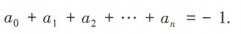2025年高职单招《数学(中职)》每日一练试题10月02日
2025-10-02 15:49:18 来源：勒克斯教育网
2025年高职单招《数学(中职)》每日一练试题10月02日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、已知椭圆C的中心为坐标原点,椭圆C的一个焦点为(1,0),且椭圆C经过点(0,
),则椭圆C的标准方程为()
- A：
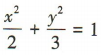
- B：
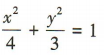
- C：
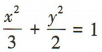
- D：
答 案：B
解 析：根据题意,椭圆的焦点在x轴上,故设椭圆的方程为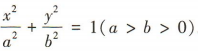
,显然半焦距c=1,短半轴长
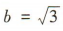,所以a2=b2+c2=4,故椭圆的方程为
2、下列函数中，最小正周期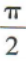
的是()
- A：
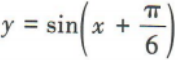
- B：
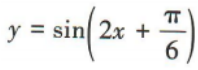
- C：
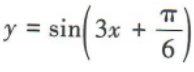
- D：
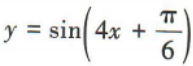
答 案：D
解 析：易知函数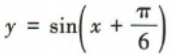
的最小正周期为
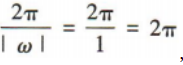,故A不符合题意；易知函数
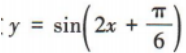的最小正周期为
，故B不符合题意；易知函数
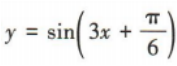的最小正周期为
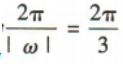,故C不符合题意；易知函数
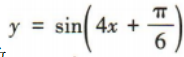的最小正周期为
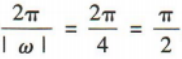,故D符合题意.
3、已知i是虚数单位,则复数z=2+i3的虚部为（）
- A：-1
- B：1
- C：0
- D：i
答 案：A
解 析：因为z=2+i3=2-i，所以z的虚部为-1.
主观题
1、已知
答 案：方法一：矢量图表示法 矢量图表示法如图所示。
方法二：矢量表示法
解 析：
填空题
1、不等式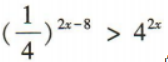
的解集为（）
答 案：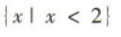
解 析：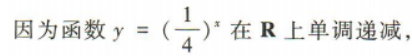
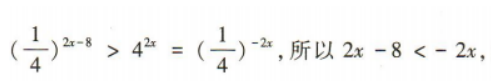
2、在等差数列{an}中,已知 a5+a8=5,则a2+a11=()
答 案：5
解 析：由等差数列的性质可知a2+a11=a5+a8=5.
3、若10件产品中有2件次品,现从中任取3件,则至少有一件是次品的取法共有（）种。
答 案：64
解 析：从 10件产品中任取3件的取法共有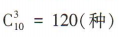
,其中一件次品都没有的取法共有
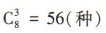,所以至少有一件次品的取法共有120-56=64(种).
简答题
1、已知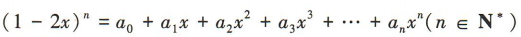
,该展开式的二项式系数之和为 32. (1)求n的值;(2)求
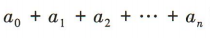的值.
答 案：(1)因为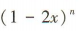
的展开式的二项式系数之和为 32, 所以2n=32,解得n=5.
(2)令x=1,得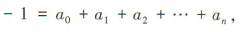
所以
- 备考交流
-
单招真题交流3群
扫一扫或点击二维码入群
