2025年高职单招《数学》每日一练试题09月20日
2025-09-20 14:40:34 来源:勒克斯教育网
2025年高职单招《数学》每日一练试题09月20日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、函数f(x)=(x-1)(x2+3x-10)有3个零点。()
答 案:对
2、若向量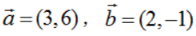 ,则向量
,则向量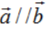 。()
。()
答 案:错
单选题
1、数列的通项公式是an=n(2n+1),则它的第7项是()
- A:115
- B:105
- C:91
- D:56
答 案:B
2、函数y=lg(x-1)的定义域为().
- A:{x|x>0}
- B:{x|x>l}
- C:{x|x≥l或x<0}
- D:{x|0
答 案:B
解 析:求y=lg(x-1)的定义域,即:使此函数的存在有意义,当lg(x-1)中x-1>0时,lg(x-1)有意义,由x-1>0,求得x>1.,所以选择B
多选题
1、已知数列{3n-1},下面选项正确的是()
- A:这个数列是公比为3的等比数列
- B:这个数列是公差为3的等差数列
- C:这个数列的第5项是14
- D:20是这个数列的第7项
答 案:BCD
解 析:已知数列{3n-1},这个数列是公差为3的等差数列,故A错误,B正确。数列第五项=3*5-1=14。故C正确。数列第七项=3*7-1=20.故D正确
2、下列四个命题中正确的是()
- A:与圆有公共点的直线是该圆的切线
- B:垂直于圆的半径的直线是该圆的切线
- C:到圆心的距离等于半径的直线是该圆的切线
- D:过圆直径的端点,垂直于此直径的直线是该圆的切线
答 案:CD
解 析:A中,与圆有两个公共点的直线,是圆的割线,故该选项不符合题意;B中,应经过此半径的外端,故该选项不符合题意;C中,根据切线的判定方法,故该选项符合题意;D中,根据切线的判定方法,故该选项符合题意。故选:CD。
主观题
1、设函数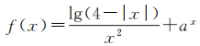 ,a>0且a≠1.
(1)求函数f(x)的定义域;
(2)若f(-3)=8,求实数a的值,并判断函数f(x)的奇偶性.
,a>0且a≠1.
(1)求函数f(x)的定义域;
(2)若f(-3)=8,求实数a的值,并判断函数f(x)的奇偶性.
答 案:(1)由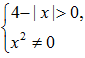 ,得
,得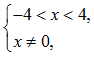 即有-4<x<0或0<x<4
因此,函数f(x)的定义域为{x|-4<x<0或0<x<4}
(2)因为
即有-4<x<0或0<x<4
因此,函数f(x)的定义域为{x|-4<x<0或0<x<4}
(2)因为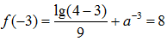 所以
所以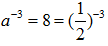 ,解得
,解得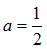 因为
因为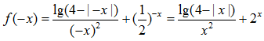 所以f(-x)≠-f(x),且f(-x)≠f(x).
因此,函数f(x)既不是奇函数也不是偶函数
所以f(-x)≠-f(x),且f(-x)≠f(x).
因此,函数f(x)既不是奇函数也不是偶函数
2、甲、乙两支球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是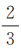 .假设各局比赛结果相互独立.
(1)分别求甲队以3:0,3:1,3:2获得比赛胜利的概率;
(2)若比赛结果为3:0或3:1,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分,对方得1分.求乙队得分
.假设各局比赛结果相互独立.
(1)分别求甲队以3:0,3:1,3:2获得比赛胜利的概率;
(2)若比赛结果为3:0或3:1,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分,对方得1分.求乙队得分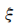 的分布列和数学期望.
的分布列和数学期望.
答 案:(1)设“甲队以3:0胜利”为事件A,“甲队以3:1胜利”为事件B,“甲队以3:2胜利”为事件C,则
 (2)
(2)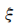 的所有可能取值为0,1,2,3,设“乙队以3:2胜利”为事件D,由于各局比赛结果相互独立,
则
的所有可能取值为0,1,2,3,设“乙队以3:2胜利”为事件D,由于各局比赛结果相互独立,
则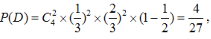
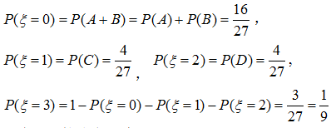 因此,
因此,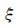 的分布列为
的分布列为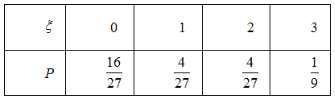
 的数学期望
的数学期望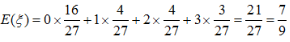
填空题
1、在菱形ABCD中,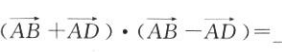 ()
()
答 案: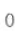
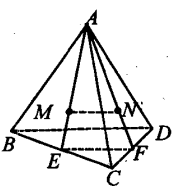
2、如图,A是∆BCD所在平面外一点,M,N分别是∆ABC和∆ACD的重心,若BD=a,则MN=_______.
答 案: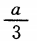
解 析: