2025年高职单招《数学》每日一练试题09月19日
2025-09-19 14:44:51 来源:勒克斯教育网
2025年高职单招《数学》每日一练试题09月19日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、函数y=sin(3x+π/2)的最大值为3。()
答 案:错
2、平面向量的加法运算只遵循平行四边形法则()
答 案:错
解 析:平面向量的加法运算有三角形法则和平行四边形法则,题目中说“只遵守”不对。
单选题
1、已知直线2x+3y-6=0,下列各点在直线上的是()
- A:(3,0)
- B:(2,4)
- C:(1,3)
- D:(5,3)
答 案:A
解 析:将各点(x,y)代入直线方程中验算。选A
2、若等差数列{an}的公差为d,且a5=3,a1+a10=10,则d=()
- A:2
- B:3
- C:4
- D:5
答 案:C
多选题
1、下列四个命题中正确的是()
- A:与圆有公共点的直线是该圆的切线
- B:垂直于圆的半径的直线是该圆的切线
- C:到圆心的距离等于半径的直线是该圆的切线
- D:过圆直径的端点,垂直于此直径的直线是该圆的切线
答 案:CD
解 析:A中,与圆有两个公共点的直线,是圆的割线,故该选项不符合题意;B中,应经过此半径的外端,故该选项不符合题意;C中,根据切线的判定方法,故该选项符合题意;D中,根据切线的判定方法,故该选项符合题意。故选:CD。
2、已知函数y=1/2sin2x则()
- A:函数最大值为2
- B:函数最大值为1/2
- C:周期
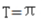
- D:周期
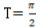
答 案:BC
解 析:A:sin2x最大值为1,则y=1/2sin2x的最大值为1/2,故A错B对。C:T=2π/W=2π/2=π,故C对D错
主观题
1、设函数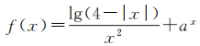 ,a>0且a≠1.
(1)求函数f(x)的定义域;
(2)若f(-3)=8,求实数a的值,并判断函数f(x)的奇偶性.
,a>0且a≠1.
(1)求函数f(x)的定义域;
(2)若f(-3)=8,求实数a的值,并判断函数f(x)的奇偶性.
答 案:(1)由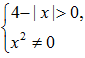 ,得
,得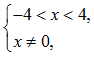 即有-4<x<0或0<x<4
因此,函数f(x)的定义域为{x|-4<x<0或0<x<4}
(2)因为
即有-4<x<0或0<x<4
因此,函数f(x)的定义域为{x|-4<x<0或0<x<4}
(2)因为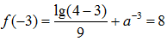 所以
所以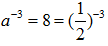 ,解得
,解得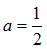 因为
因为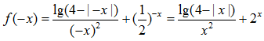 所以f(-x)≠-f(x),且f(-x)≠f(x).
因此,函数f(x)既不是奇函数也不是偶函数
所以f(-x)≠-f(x),且f(-x)≠f(x).
因此,函数f(x)既不是奇函数也不是偶函数
2、某投资商计划用60万元投资甲、乙两个项目.根据预判,甲项目最大亏损率为20%,乙项目最大亏损率为30%,最大亏损不能超过16万元;甲、乙两个项目的最大盈利率分别为70%和60%.问投资商对甲、乙两个项目分别投资多少万元时,才能使盈利最大?最大盈利是多少万元?
答 案:设投资商对甲、乙两个项目分别投资x,y万元,获得的盈利为z万元,则有 目标函数z=0.7x+0.6y,
作可行域,如图所示:
目标函数z=0.7x+0.6y,
作可行域,如图所示:
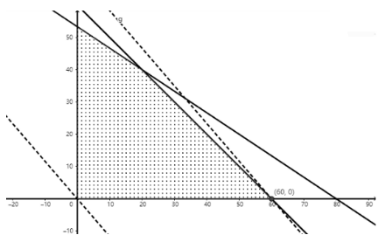 作0等值线l0:0.7x+0.6y=0,并平移0等值线,当直线l0经过可行域中的点(60,0)时,目标函数z取到最大值
所以,当x=60,y=0时,最大盈利为0.7×60+0.6×0=42(万元)
因此,投资商对甲、乙两个项目分别投资60万元和0万元才能使盈利最大,最大盈利为42万元
作0等值线l0:0.7x+0.6y=0,并平移0等值线,当直线l0经过可行域中的点(60,0)时,目标函数z取到最大值
所以,当x=60,y=0时,最大盈利为0.7×60+0.6×0=42(万元)
因此,投资商对甲、乙两个项目分别投资60万元和0万元才能使盈利最大,最大盈利为42万元
填空题
1、从甲、乙、丙3人中任选2人参加社会实践,甲被选中的概率为_______
答 案:2/3
2、已知α的终边经过点P(3m,-4m),若m>0,则sinα =______,cosα =______,tanα=______.
答 案: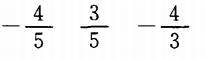
解 析:∵m>0,角α的终边经过点P(3m,-4m),
∴x=3m,y=-4m,r=5m
∴sinα=y/r=-4/5,cosα=x/r=3/5
tanα=sinα/cosα=-4/3



