2025年高职单招《数学(中职)》每日一练试题08月18日
2025-08-18 15:49:37 来源：勒克斯教育网
2025年高职单招《数学(中职)》每日一练试题08月18日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、记Sn为等比数列{an}的前n项和，若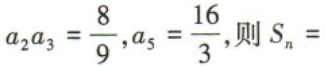
（）
- A：
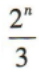
- B：
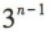
- C：
- D：
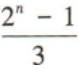
答 案：D
解 析：
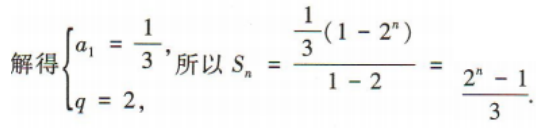
2、设向量a=(t,-6),b=(-3,2).若a//b,则实数为()
- A：-9
- B：-3
- C：3
- D：9
答 案：D
解 析：因为a//b,所以2t-(-3)×(-6)=0,解得t=9。
3、在△ABC中，内角A,B,C的对边分别为a,b,c,若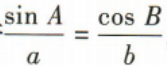
则B=（）
- A：
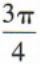
- B：
- C：
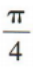
- D：
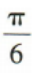
答 案：C
解 析：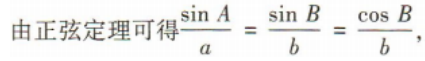
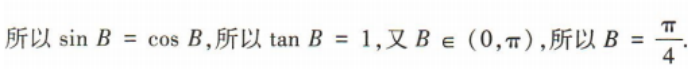
主观题
1、已知
答 案：方法一：矢量图表示法 矢量图表示法如图所示。
方法二：矢量表示法
解 析：
填空题
1、已知等差数列{an}的前n项和为 Sn,S3=9,a4 + a5+a6=7,则S9-S6=()
答 案：5
解 析：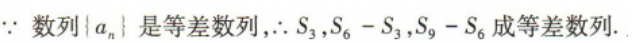
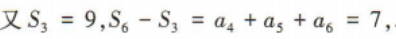
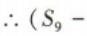
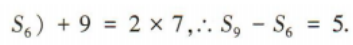
2、已知集合A={x|x<2a-1},B={x|x≥1},且A∪B=R,则实数a的取值范围是（）
答 案：a≥1
解 析：由A∪B=R,A={x|x<2a-1},B={x|x≥1}得2a-1≥1,解得a≥1.
3、已知△ABC中，∠A，∠B，∠C所对边为a，b，c，C=30°,a=c=2,则b=____.
答 案：2√3
解 析：a=c=2, 所以A=C=30°,B=120°, 所以b2=a2+c2-2accosB=12， 所以b= 2√3
简答题
1、已知数列{an}是等差数列，a1=1,a3=3. (1)求数列{an}的通项公式； (2)设bn=(-1)nan,数列{bn}的前n项和为Tn,求T100
答 案：
温馨提示：因考试政策、内容不断变化与调整，本站提供的以上信息仅供参考，如有异议，请考生以权威部门公布的内容为准！
- 备考交流
-
单招真题交流3群
扫一扫或点击二维码入群
热门资讯
相关试卷
猜你喜欢
换一换
2025年四川高职单招考试时间表
01-09
2025年湖南高职单招报名公告查询
01-09
山东综评报名时间2025具体时间
01-08
山东综评什么时候考试2025年 山东综评招生考试时间
01-08
山东高职单招报名时间2025年
01-07
2025年山东单招综评学校有哪些 山东综合评价招生学校名单汇总
01-07
黑龙江省2025年高职院校单独招生考试有关工作安排的通知
12-28
黑龙江2025年高职单招考试时间及科目安排
12-26
