2024年高职单招《数学(中职)》每日一练试题12月02日
2024-12-02 16:07:18 来源:勒克斯教育网
2024年高职单招《数学(中职)》每日一练试题12月02日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、下列说法正确的是()
- A:若一个平面中有无数条直线与另一个平面平行,则这两个平面平行
- B:若两条不同直线都与第三条直线垂直,则这两条直线互相平行
- C:两相交直线确定一个乎面
- D:各个面都是三角形的几何体一定是棱锥
答 案:C
解 析:若一个平面中有无数条直线与另一个平面平行,则这两个平面平行或相交,故A错误,若两条不同直线都与第三条直线垂直,则这两条直线平行或相交或异面,故B错误,易知两相交直线可以确定一个平面,故C正确.如图所示的几何体不是棱锥且各个面都是三角形,故D错误. 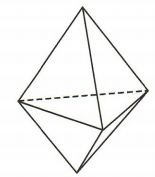
2、在等比数列{an}中,a2=9,a5=243,则{an}的前4项和为()
- A:81
- B:120
- C:168
- D:192
答 案:B
解 析:设等比数列{a}的公比为q.由题意得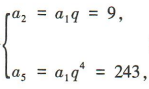 解得a1=3,q=3,故a3=a2q=27,a4=a3q=81,所以{a,}的前4项和S4=a1+a2+a3+a4=3+9+27+81=120.
解得a1=3,q=3,故a3=a2q=27,a4=a3q=81,所以{a,}的前4项和S4=a1+a2+a3+a4=3+9+27+81=120.
3、已知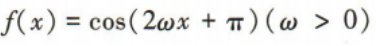 ,则下列说法正确的是()
,则下列说法正确的是()
- A:若f(x)的最小正周期为π,则ω=2
- B:若f(x)的最小正周期为π,则ω=1
- C:若x=0,则f(x)的值为0
- D:若x=0,则f(x)取得最大值-1
答 案:B
解 析: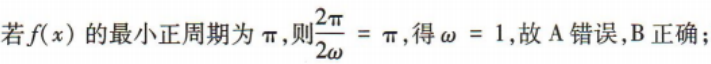 若x=0,则f(x)=cosπ=-1,且为最小值,故C,D错误.
若x=0,则f(x)=cosπ=-1,且为最小值,故C,D错误.
4、已知A(2,-3),B(3,-2),直线l的方程为mx+y+1=0,若直线l//AB,则m=()
- A:-1
- B:1
- C:-2
- D:2
答 案:A
解 析:由 A(2,- 3),B(3,- 2),得直线AB的斜率为1.又直线l的方程为mx+y+1=0,直线l// AB,所以直线l的斜率k=-m=1,故m=-1.
填空题
1、若椭圆上一点到两焦点F1(-2,0),F2(2,0)的距离之和为8,则该椭圆的短轴长为()
答 案: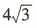
解 析:由题知c= 2,2a=8,即a=4,故b2=a2-c2=12,得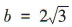 ,所以该椭圆的短轴长为
,所以该椭圆的短轴长为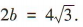
2、函数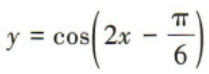 的最小正周期为()
的最小正周期为()
答 案:π
解 析:
3、(1-ax)6的展开式中x3的系数为 20,则a的值为()
答 案:-1
解 析:易知(1-ax)6的展开式中x3 的系数为 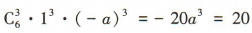 ,解得a=-1.
,解得a=-1.
4、已知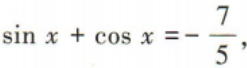 则sin2x=()
则sin2x=()
答 案: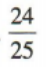
解 析: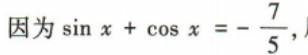
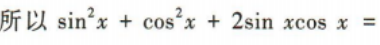

简答题
1、已知命题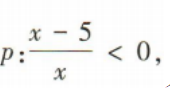 命题q:y=log2(x2-x-12)有意义.若p∧q为真命题,求实数x的取值范围.
命题q:y=log2(x2-x-12)有意义.若p∧q为真命题,求实数x的取值范围.
答 案:由 2、已知四边形 ABCD 为平行四边形,A(-2,1),B(4,0),D(-2,11).
(1)求点C的坐标;(2)若点P满足 答 案:(1)设点C的坐标为(a,b),则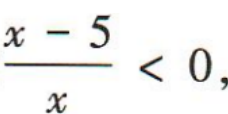 得0
得0 解得4
解得4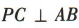 ,求直线 PC 的方程.
,求直线 PC 的方程.
 因为四边形 ABCD 为平行四边形,
所以
因为四边形 ABCD 为平行四边形,
所以 所以
所以 解得
解得 所以点C的坐标为(4,10).
(2)由题意可得直线AB的斜率
所以点C的坐标为(4,10).
(2)由题意可得直线AB的斜率 设直线 PC 的方程为y= kx+b.
因为
设直线 PC 的方程为y= kx+b.
因为 所以kABk=-1,解得k= 6.
将C(4,10)代入y=6x+b中,得10=24+b,解得b=- 14,
所以直线PC的方程为y=6x-14,即6x-y-14 =0.
所以kABk=-1,解得k= 6.
将C(4,10)代入y=6x+b中,得10=24+b,解得b=- 14,
所以直线PC的方程为y=6x-14,即6x-y-14 =0.



