2025年成考专升本《高等数学二》每日一练试题01月22日
2025-01-22 11:49:18 来源：勒克斯教育网
2025年成考专升本《高等数学二》每日一练试题01月22日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、设函数y=f（x）在点（x，f（x））处的切线斜率为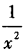
，则过点（1，0）的切线方程为（）。
- A：
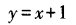
- B：
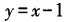
- C：
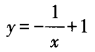
- D：
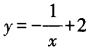
答 案：B
解 析：本题考查的知识点是：函数y=f（x）在点（x，f（x））处导数的几何意义是表示该函数对应曲线过点（x，f（x））的切线的斜率。由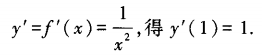
可知，切线过点（1，0），则切线方程为y=x-1，所以选B。
2、已知函数f(x)在x=2处可导，且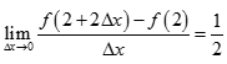
，则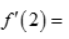
（）。
- A：
- B：
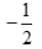
- C：
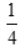
- D：
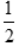
答 案：C
解 析：根据导数的定义式可知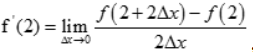
，故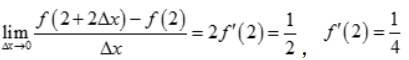
主观题
1、在半径为R的半圆内作一内接矩形，其中的一边在直径上，另外两个顶点在圆周上（如图所示）．当矩形的长和宽各为多少时矩形面积最大？最大值是多少？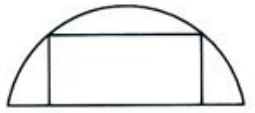
答 案：解：如图所示
，设x轴通过半圆的直径，y轴垂直且平分直径．设OA＝x，则AB＝
，矩形面积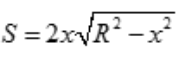
．
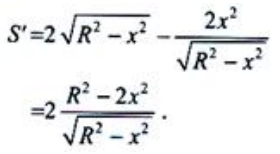令s'=0，得
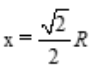（舍去负值）．
由于只有唯一驻点，根据实际问题x＝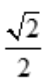
，必为所求，则AB＝
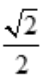R．所以，当矩形的长为
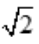R、宽为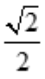
R时，矩形面积最大，且最大值S＝R2．
2、某班有党员10人，其中女党员有6人，现选3人组成党支部．设事件A＝{党支部中至少有1名男党员}，求P（A）．
答 案：解：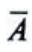
＝{党支部中没有男党员}，则
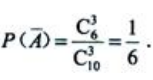因为
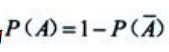，所以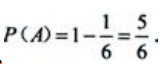
填空题
1、设f(x)是可导的偶函数，
＝k≠0，则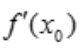
＝（）．
答 案：-k
解 析：由f(x)是偶函数，得f(-x)＝f(x)，则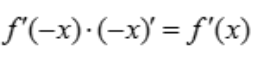
，即
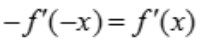，故
．
2、函数y=x-ln（1+x）的驻点为x=______。
答 案：0
解 析：本题考查的知识点是驻点的概念及求法。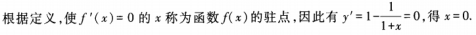 
故填0。
简答题
1、设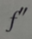
存在，
答 案：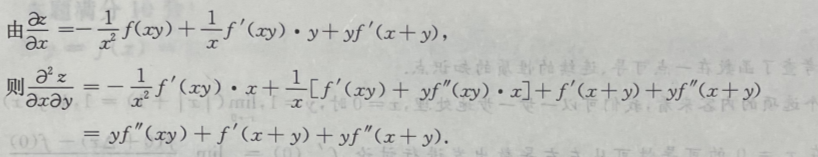
2、设事件A与B相互独立，且P（A）=0.6，P（B）=0.7，求P（A+B）。
答 案：本题考查事件相互独立的概念及加法公式。 
- 备考交流
-
2025成考内部交流群群号：665429327
扫一扫或点击二维码入群
