2025年成考高起点《数学(文史)》每日一练试题11月19日

2025年成考高起点《数学(文史)》每日一练试题11月19日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、一个袋子中装有标号分别为1，2，3，4的四个球，采用有放回的方式从袋中摸球两次，每次摸出一个球，则恰有一次摸出2号球的概率为（）。

• A：
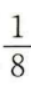
• B：
• C：
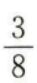
• D：

答 案：C

解 析：本题主要考查的知识点为独立重复试验的概率。 所求概率为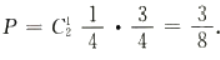

2、已知M为椭圆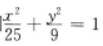上的一点，F₁,F₂是椭圆的两个焦点，且∠F₁MF₂=60°，则△F₁MF₂的面积为（）

• A：
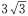
• B：3
• C：
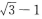
• D：

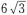
答 案：A

解 析：由椭圆方程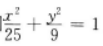 知，长轴长2a=10，焦距2c=8，设|MF1|=t，由余弦定理8²=t²+（10-t）²-2t（10-t）cos60°，得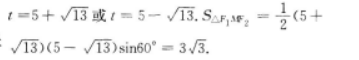

3、已知圆的半径为R，弧长为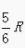的弧所对的圆心角等于（）。

• A：
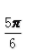
• B：
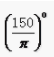
• C：1200
• D：

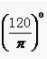
答 案：B

4、直线l₁与直线l₂：3x+2y-12=0的交点在x轴上，并且l₁⊥l₂，则l₁在y轴上的截距是（）。

• A：-4
• B：
• C：4
• D：

答 案：B

解 析：由于直线l2:3x+2y-12=0与x轴的交点为（4,0），斜率为故直线l1的斜率为，且经过（4,0），故l1的方程为y-0=令x=0求得，即l1在y轴上的截距是故选C。 用点斜式求得直线l1的方程，再根据直线在y轴上的截距的定义求得l1在y轴上的截距，本题主要考查用点斜式求直线的方程，直线在y轴上的截距的定义和求法，属于基础题

主观题

1、

答 案：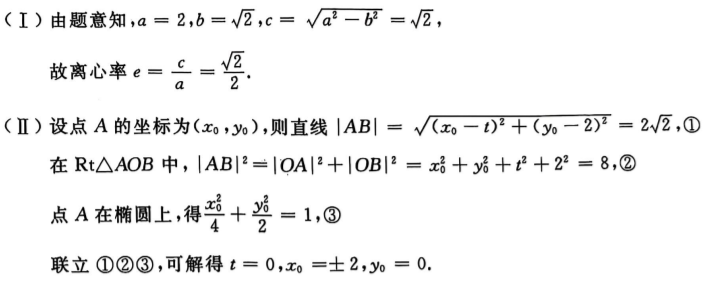

解 析：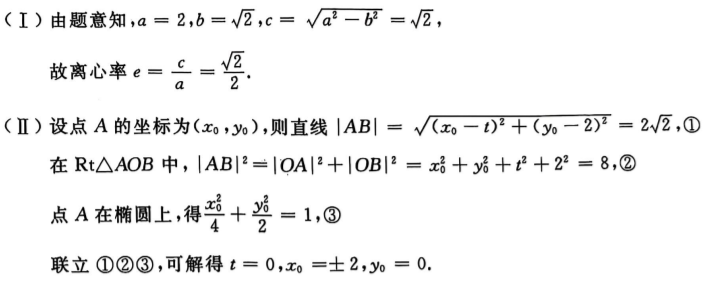

2、弹簧的身长与下面所挂砝码的重量成正比，知弹簧挂20g重的砝码时长度是12cm,挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度

答 案：设弹簧原长为y0cm，则弹簧伸长量为（y-y0）cm， 由题意得y-y0=kx,即y=kx+y0, 由已知条件得 解得k=0.2，y0=8. 所求函数关系式为y=0.2x+8，弹的原长为8CM  

3、设椭圆的中心是坐标原点,长轴在x轴上,离心率已知点P到圆上的点的最远距离是求椭圆的方程  

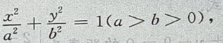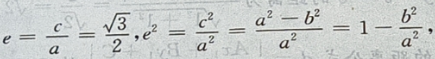
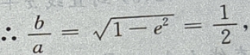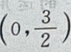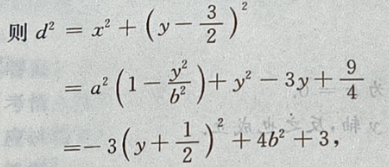
答 案：由题意，设椭圆方程为 由 设P点到椭圆上任一点的距离为 d, 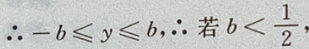则在y=-b时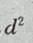，最大，即d也最大。  

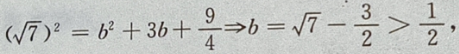
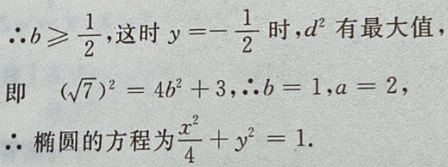
4、求下列函数的最大值、最小值和最小正周期： （1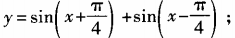） 2）y=6cosx+8sinx

答 案： 所以函数的最大值是最小值是最小正周期为2π， （2）要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式，需使cosx与sinx的系数平方和为1，为此，将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π

填空题

1、平面内有10个点，任何三点都不在同一直线上，问能连成______条不同的直线。  

答 案：45

2、化简sin（x+y）-2cosxsiny=______。  

答 案：sin（x-y）

解 析：原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin（x-y）