2025年成考高起点《数学(文史)》每日一练试题11月10日

2025年成考高起点《数学(文史)》每日一练试题11月10日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、如果点A（1，1）和B（2，4）关于直线y=kx+b对称，则k=（）。  

• A：-3
• B：
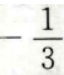
• C：
• D：3

答 案：B

解 析：本题主要考查的知识点为两垂直直线斜率的关系。 直线AB的斜率为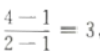：点A、B关于直线y=kx+b对称，因此直线AB与其垂直，故3k=-1，得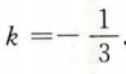

2、下列函数中，为奇函数的是（）。  

• A：y=x³
• B：y=-x³-1
• C：
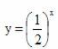
• D：

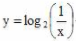
答 案：A

3、设M=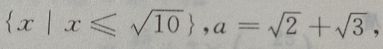那么（）

• A：
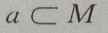
• B：
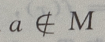
• C：
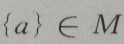
• D：

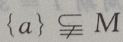
答 案：D

解 析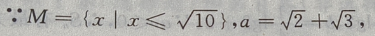： M是集合，a为元素，{a}为集合，元素与集合的关系是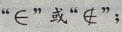集合与集合的关系是  

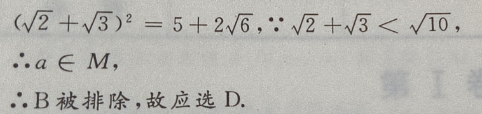
4、过点A（1，-1），B（-1，1）且圆心在直线x+y-2=0上的圆的方程是（）。

• A：（x-3）2+（y+1）2=4
• B：（x+3）2+（y-1）2=4
• C：（x-1）2+（y-1）2=4
• D：（x+1）2+（y+1）2=4

答 案：C

主观题

1、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

2、求证：双曲线的一个焦点到一条渐近线的距离等于虚半轴的长．  

答 案：设双曲线的方程为 则它的焦点坐标为F1(-c,0),F2(c,0),其中c²=a²+b²,渐近线方程为 令设焦点F2(c,0)到渐近线 的距离为d,则 即从双曲线的一个焦点F2(c,0)到一条渐近线的距离等于虚半 轴的长b，由上述推导过程可知，点F2到渐近线以及点F1(-c,0)到渐近线 的距离都等。 由于证明中只涉及a，b，c，而与双曲线的位置无关，所以这个结论对于任意双曲线都成立．

解 析：本题考查的是圆锥曲线与直线位置关系的推理能力，主要是用代数的方法表示几何中的问题．考生必须对曲线方程、几何性质及元素之间的关系有深刻的理解，方可解决此类综合题．这种综合性的圆锥曲线试题出现的概率比较高，要引起重视．

3、设3^a=5^b=15，求a^-1+b^-1的值。  

答 案：由3^a=15，得a=log₃15；又由5^b=15，得b=log₅15。 因此a^-1+b^-1=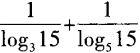 =log₁₅3+log₁₅5=1。

解 析：过程中应用了换底公式的推论，即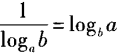

4、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.  

答 案：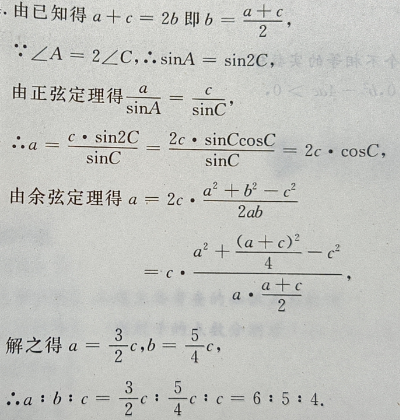

填空题

1、10^1-lg2=______。  

答 案：5

解 析：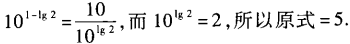  

2、已知α+β=π/4，则（1+tanα）（1+tanβ）=______。  

答 案：2