2025年成考高起点《数学(文史)》每日一练试题10月03日

2025年成考高起点《数学(文史)》每日一练试题10月03日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若a，b，c分别表示△ABC的顶点A，B，C所对的边长，且（a+b+c）（a+b-c）=3ab，cos（A+B）=（）。

• A：
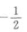
• B：
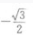
• C：
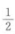
• D：

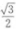
答 案：A

2、从15名学生中选出两人担任正、副班长，不同的选举结果共有（）  

• A：30种
• B：90种
• C：210种
• D：225种

答 案：C

解 析：由已知条件可知本题属于排列问题，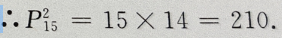

3、掷两颗骰子点数之和等于4的概率是（）。

• A：
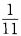
• B：
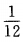
• C：
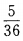
• D：

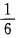
答 案：B

解 析：掷一对骰子的等可能结果共有n=36种，点数之和等于4的结果有1+3=4，3+1=4，2+2=4，故有m=3种，所以其概率为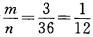故选B。  

4、从15名学生中选出两人担任正副组长，不同的选举结果共有（）。

• A：30种
• B：90种
• C：210种
• D：225种

答 案：C

主观题

1、

答 案：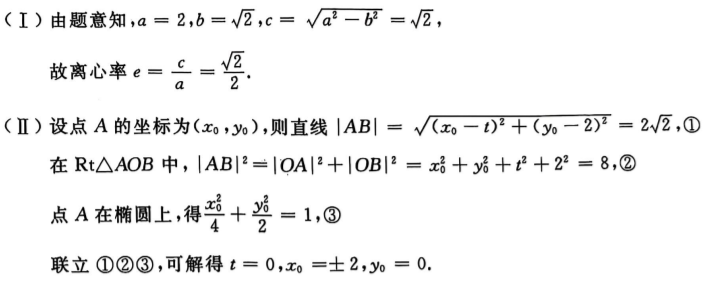

解 析：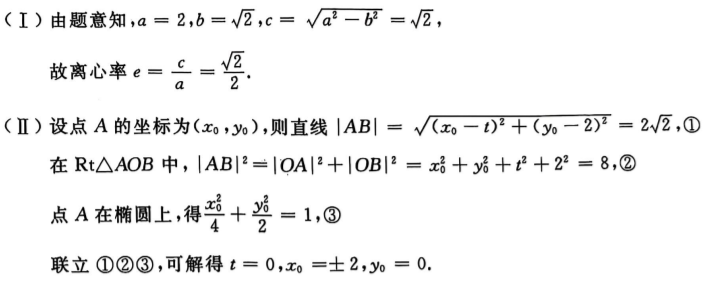

2、求证：双曲线的一个焦点到一条渐近线的距离等于虚半轴的长．  

答 案：设双曲线的方程为 则它的焦点坐标为F1(-c,0),F2(c,0),其中c²=a²+b²,渐近线方程为 令设焦点F2(c,0)到渐近线 的距离为d,则 即从双曲线的一个焦点F2(c,0)到一条渐近线的距离等于虚半 轴的长b，由上述推导过程可知，点F2到渐近线以及点F1(-c,0)到渐近线 的距离都等。 由于证明中只涉及a，b，c，而与双曲线的位置无关，所以这个结论对于任意双曲线都成立．

解 析：本题考查的是圆锥曲线与直线位置关系的推理能力，主要是用代数的方法表示几何中的问题．考生必须对曲线方程、几何性质及元素之间的关系有深刻的理解，方可解决此类综合题．这种综合性的圆锥曲线试题出现的概率比较高，要引起重视．

3、弹簧的身长与下面所挂砝码的重量成正比，知弹簧挂20g重的砝码时长度是12cm,挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度

答 案：设弹簧原长为y0cm，则弹簧伸长量为（y-y0）cm， 由题意得y-y0=kx,即y=kx+y0, 由已知条件得 解得k=0.2，y0=8. 所求函数关系式为y=0.2x+8，弹的原长为8CM  

4、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。

答 案：(I)由题意,该抛物线的焦点到准线的距离为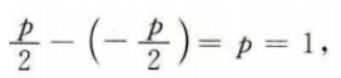 所以抛物线C的方程为y²=2x. (Ⅱ)因A(l,m)(m>0)为C上一点,故有m²=2, 可得 m=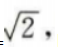因此A点坐标为 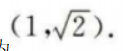设B点坐标为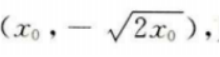

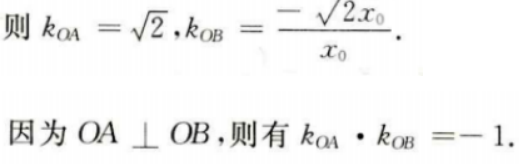
填空题

1、直线的倾斜角的度数为（）  

答 案：60°

解 析：由题意知直线的斜率为设直线的倾斜角为α，则tanα=由0°≤α≤180°，故α=60°

2、在等比数列中，a₁=3，a_n=96，S_n=189，则公比q=______，项数n=_______。  

答 案：q=2，n=6

解 析：解法一：An=A1×q^(n-1)=3q^(n-1)=96q^(n-1)=32S(n-1)=Sn-An=189-96=93
S(n-1)=A1×(1-q^(n-1))/(1-q)
=3(1-32)/(1-q)=93
q=2
2^(n-1)=32
n=6 解法二：