2025年成考高起点《数学(文史)》每日一练试题08月18日
2025-08-18 12:13:45 来源:勒克斯教育网
2025年成考高起点《数学(文史)》每日一练试题08月18日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、圆C1:x2+y2=1与圆C2:x2+y2-4x=0的位置关系是()。
- A:外切
- B:内切
- C:相交
- D:相离
答 案:C
2、用列举法表示集合{(x,y)|x+2y=7且x,y为正整数},结果是()。
- A:{x=5,3,1,y=1,2,3}
- B:{(5,1),(3,2)(1,3)}
- C:{(1,5),(2,3),(3,1)}
- D:{(7,0)(5,1)(3,2)(1,3)}
答 案:B
3、若|a|=1,|b|=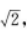 (a-b)⊥a,则a与b的夹角为( )
(a-b)⊥a,则a与b的夹角为( )
- A:30°
- B:45°
- C:60°
- D:75°
答 案:B
解 析:因为(a-b)⊥a, 【考点指要】本题考查向量的模与夹角的计算、向量的数量积的几何意义及对垂直问题的应用
【考点指要】本题考查向量的模与夹角的计算、向量的数量积的几何意义及对垂直问题的应用
4、函数的最小正周期和最大值分别为
- A:

- B:
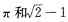
- C:
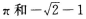
- D:
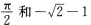
答 案:B
解 析: 【考点指要】本题考查的是三角函数y=Asin(ωx+φ)+B的周期性和最值问题,需要注意的是正弦函数y=sinx和余弦函数y=cosx的最小正周期为2π,正切函数y=tanx的最小正周期为x.
【考点指要】本题考查的是三角函数y=Asin(ωx+φ)+B的周期性和最值问题,需要注意的是正弦函数y=sinx和余弦函数y=cosx的最小正周期为2π,正切函数y=tanx的最小正周期为x.
主观题
1、已知a-a-1=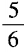 ,求a3-a-3的值。
,求a3-a-3的值。
答 案:
2、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
3、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
答 案:由已知,得 
4、设全集U=R,集合A={x|-5<x<5},B={x|0≤x≤7},求CUA∩B.
答 案:解:全集U=R,A={x|-5<x<5},B={X|0≤x≤7},因为CuA={x|x≤-5或x≥5},所以CuA∩B={x|x≤-5或x≥5}N{x|0≤x≤7}={x|5≤x≤7},如图1—10所示。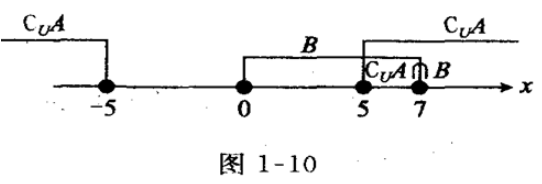
填空题
1、化简sin(x+y)-2cosxsiny=______。
答 案:sin(x-y)
解 析:原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin(x-y)
2、在△ABC中,AB=1, ______。
______。
答 案: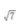
2024年成考高起点《数学(文史)》每日一练试题08月18日 08-18 2023年成考高起点《数学(文史)》每日一练试题08月18日 08-18 2025年成考高起点《数学(文史)》每日一练试题10月18日 10-18 2025年成考高起点《数学(文史)》每日一练试题01月18日 01-18 2025年成考高起点《数学(文史)》每日一练试题04月18日 04-18 2025年成考高起点《数学(文史)》每日一练试题05月18日 05-18 2025年成考高起点《数学(文史)》每日一练试题06月18日 06-18 2025年成考高起点《数学(文史)》每日一练试题03月18日 03-18



