2025年成考高起点《数学(文史)》每日一练试题07月02日

2025年成考高起点《数学(文史)》每日一练试题07月02日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、函数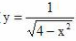的定义域为（）。

• A：（-∞，-4）∪（4，+∞）
• B：（-∞，-2）∪（2，+∞）
• C：[-2，2]
• D：（-2，2）

答 案：D

2、如果方程lg2x+(lg2+lg3)lgx+lg2×lg3=0的两个根分别是x1，x2，那么x1·x2=（　）

• A：lg2×lg3
• B：lg2+lg3
• C：1/6
• D：-6

答 案：C

解 析：【考点指要】本题考查一元二次方程的有关知识及对数的运算法则．注意此方程不是关于2的二次方程，是关于lgx的二次方程，因此运用韦达定理时需要写成lgx1+lgx2与lgx1·lgx2，最好采用题解中换元的方法．

3、过点A（1，-1），B（-1，1）且圆心在直线x+y-2=0上的圆的方程是（）。

• A：（x-3）2+（y+1）2=4
• B：（x+3）2+（y-1）2=4
• C：（x-1）2+（y-1）2=4
• D：（x+1）2+（y+1）2=4

答 案：C

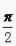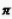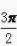4、cos+cos（-）+cot+sin+tan=（）。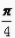

• A：2
• B：1
• C：-2
• D：-1

答 案：D

主观题

1、已知函数ƒ(x)=ax3-x2+bx+1(a，b∈R)在区间(-∞，0)和(1，+∞)上都是增函数，在(0，1)内是减函数． (Ⅰ)求a，b的值； (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程．

答 案：(Ⅰ)因为函数ƒ(x)在(-∞，0)上递增，在（0,1）内递减，在（1，+∞）上有递增，可知函数在x=0和x=1处的导数值均为0. 又f’(x)=3ax²-2x+b, 所以f’(0)=b=0,f’(1)=3a-2+b=0. 即切点为(3.10),所以其切线方程为y-10=12(x-3),即12x-y-26 = 0.  

解 析：【考点指要】本题主要考查函数导数的几何意义、导数的求法和导数的应用——函数的单调区间及曲线的切线方程的求法  

2、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

3、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：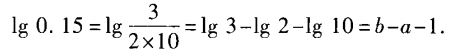

4、cos20°cos40°cos80°的值。  

答 案：

填空题

1、在△ABC中，已知AB=3，BC=5，AC=7，则cosB=______。

答 案：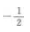

2、已知tanα=2，则=______。  

答 案：