2025年高职单招《数学》每日一练试题12月07日

2025年高职单招《数学》每日一练试题12月07日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、过点(0,1)且与直线2x-y=0垂直的直线方程的一般式是y=-2x+1。()  

答 案：错

2、一篮球运动员在六场比赛中所得到的分数分别为15,16,11,14,12,13,则该运动员所得分数的中位数是14。()  

答 案：错

单选题

1、如果b>a>0,那么().

• A：
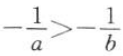
• B：
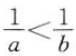
• C：
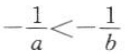
• D：-b>-a

答 案：C

解 析：采用取特殊值法，可知选项C正确.

2、函数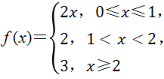的值域是(　　)  

• A：R
• B：[0，2]∪{3}
• C：[0，＋∞)
• D：[0，3]

答 案：B

解 析：当0≤x≤1时，0≤2x≤2，即0≤f(x)≤2；当1＜x＜2时，f(x)＝2；当x≥2时，f(x)＝3.综上可知f(x)的值域为[0，2]∪{3}.

多选题

1、设{a_n}(n∈N^*)是各项为正数的等比数列，q是其公比，K_n是其前n项的积，且K₅K₈，则下列选项中成立的是()  

• A：0
• B：a₇＝1
• C：K₉>K₅
• D：K₆与K₇均为K_n的最大值

答 案：ABD

解 析：根据题意，依次分析选项：
对于B，若K6＝K7，则a7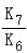＝＝1，故B正确；
对于A，由K5＜K6可得a6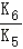＝＞1，则q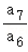＝∈（0，1），故A正确；
对于C，由{an}是各项为正数的等比数列且q∈（0，1）可得数列单调递减，则有K9＜K5，故C错误；
对于D，结合K5＜K6，K6＝K7＞K8，可得D正确．
故选：ABD．

2、已知函数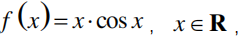则下列说法正确的有（  ）  

• A：是奇函数
• B：是周期函数
• C：曲线在点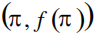处的切线方程为 x + y = 0
• D：在区间上，单调递增

答 案：AC

解 析：利用奇函数的定义可以判定函数 f (x) 是奇函数，所以选项 A 正确；不存在非零常数T ，使得 f (x + T ) = f (x) ，故 f (x) 不是周期函数，所以选项 B 错误；f (x) 在点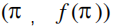处的切线方程为 x+y=0，所以选项 C 正确； 利用导数可以判定函数 f (x) 在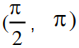单调递减，所以选项 D 错误.

主观题

1、在等差数列{a_n}中,a₅=-10,a₁₀=0.
(1)求数列{a_n}的通项公式;
(2)记数列{a_n}的前n项和为S_n;
当n为何值时，S_n有最小值?最小值是多少?  

答 案：（1）设等差数列{a_n}的公差为d， 则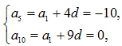解得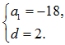 因此，数列{a_n}的通项公式为a_n=-18+2(n-1)，即a_n=2n-20 （2）由等差数列的前n项和公式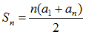得 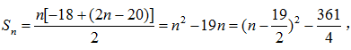所以当n=9或n=10时，S_n有最小值-90  

2、已知函数f（x）＝ae^x﹣lnx﹣1． （1）设x＝2是f（x）的极值点，求a，并求f（x）的单调区间； （2）证明：当a≥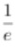时，f（x）≥0．

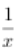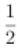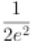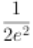答 案：解：（1）∵函数f（x）=ae^x-lnx-1． ∴x＞0，f′（x）=ae^x-， ∵x=2是f（x）的极值点， ∴f′（2）=ae²-=0，解得a=， ∴f（x）=e^x-lnx-1， ∴f′（x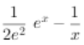）=，显然f′（x）在（0，+∞）上单调递增， ∴当0＜x＜2时，f′（x）＜0，当x＞2时，f′（x）＞0， ∴f（x）在（0，2）单调递减，在（2，+∞）单调递增． （2）证明：当a≥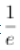时，f（x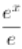）≥-lnx-1， 设g（x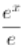）=-lnx-1，则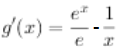， 由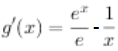=0，得x=1，且g’(x)在（0，+∞）上单调递增， 当0＜x＜1时，g′（x）＜0， 当x＞1时，g′（x）＞0， ∴x=1是g（x）的极小值点，也是最小值点， 故当x＞0时，g（x）≥g（1）=0， ∴当a≥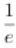时，f（x）≥0．

填空题

1、若曲线 y＝x2－1 的一条切线平行于直线 y＝4x－3，则这条切线的方程为________.  

答 案：4x－y－5＝0

解 析：y′＝2x，设切点为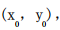则由题意可知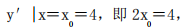，所以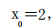 代入曲线方程得 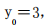故该切线过点(2,3)且斜率为 4，所以这条切线方程为 y－3＝4(x－2)，即 4x－y－5＝0.  

2、已知一元二次不等式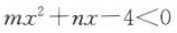的解集是(-2,4),则mn=（）.

答 案：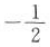

解 析：二次方程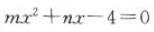的两个解分别为x1=-2,x2=4,用根与系数关系可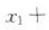得,解得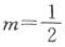,n=-1,所以