2025年高职单招《数学》每日一练试题11月28日

2025年高职单招《数学》每日一练试题11月28日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、平面向量的加法运算遵循三角形法则。（）  

答 案：错

解 析：平面向量的加法运算遵循平行四边形法则和三角形法则。

2、奇函数的图像关于y轴对称。（）  

答 案：错

解 析：奇函数原点对称，所以错误

单选题

1、设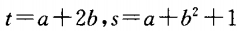，则下列s与t的关系中正确的是（）。  

• A：
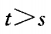
• B：
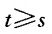
• C：
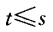
• D：

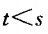
答 案：C

解 析：∵t=a+2b，s=a+b²+1， ∴s-t=(a+b²+1)-(a+2b)=b²-2b+1=(b-1)²≥0， ∴s≥t. 本题是一道关于代数式的比较大小的题目，分析题意，尝试利用作差法进行解答；
根据题意，分析t和s的表达式，可用s减去t，进行整理可得b2-2b+1；
接下来，利用完全平方的和平方项的非负性即可解答本题

2、已知数列的通项公式为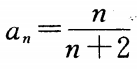，下列命题正确的是（）  

• A：1/3是它的一项
• B：5/9是它的一项
• C：1/3和5/9都是它的项
• D：9/11和5/9都不是它的项

答 案：A

解 析：

多选题

1、已知点P到圆O上的点的最大距离是7cm，最小距离是1m，则圆O的半径是（）  

• A：4cm
• B：3cm
• C：5cm
• D：6cm

答 案：AB

2、下列说法不正确的是（）  

• A：相切两圆的连心线经过切点
• B：长度相等的两条弧是等弧
• C：平分弦的直径垂直于弦
• D：相等的圆心角所对的弦相等

答 案：BCD

解 析：A、根据圆的轴对称性可知此命题正确，不符合题意；B、等弧指的是在同圆或等圆中，能够完全重合的弧．而此命题没有强调在同圆或等圆中，所以长度相等的两条弧，不一定能够完全重合，此命题错误，符合题意；C、此弦不能是直径，命题错误，符合题意；D、相等的圆心角指的是在同圆或等圆中，此命题错误，符合题意；故选：BCD

主观题

1、某旅游景点预计2017年1月份起前x个月的旅游人数的和p(x)(单位：万人)与x的关系近似地满足p(x)＝x(x＋1)(39－2x)(x∈N*，且x≤12).已知第x个月的人均消费额q(x)(单位：元)与x的近似关系是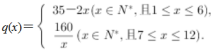 (1)写出2017年第x个月的旅游人数f(x)(单位：人)与x的函数关系式； (2)试问2017年第几个月旅游消费总额最大？最大月旅游消费总额为多少元？

答 案：解：(1)当x＝1时，f(1)＝p(1)＝37，当2≤x≤12，且x∈N*时， f(x)＝p(x)－p(x－1)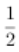＝x(x＋1)(39－2x)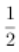－(x－1)x(41－2x)＝－3x2＋40x， 验证x＝1也满足此式，所以f(x)＝－3x2＋40x(x∈N*，且1≤x≤12). (2)第x个月旅游消费总额为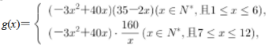 即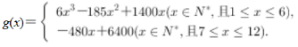 ①当1≤x≤6，且x∈N*时， g′(x)＝18x2－370x＋1400， 令g′(x)＝0，解得x＝5或x＝(舍去). 当1≤x＜5时，g′(x)＞0， 当5＜x≤6时，g′(x)＜0， ∴当x＝5时，g(x)max＝g(5)＝3125(万元). ②当7≤x≤12，且x∈N*时， g(x)＝－480x＋6400是减函数， ∴当x＝7时，g(x)max＝g(7)＝3040(万元). 综上，2017年5月份的旅游消费总额最大，最大旅游消费总额为3125万元.

2、设函数f（x)=ax³-2bx²+cx+4d（a、b、c、d∈R）图象关于原点对称，且x=1时，f（x）取极小值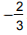 （1）求a、b、c、d的值： （2）当x∈[-1，1]时，图象上是否存在两点，使得过此两点处的切线互相垂直？试证明你的结论： （3）若x₁，x₂∈[-1,1]时，求证：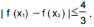

答 案：（1）函数f(x)图象关于原点对称，∴对任意实数x有f（x)=-f（x)， ∴-ax³-2bx²-cx+4d=-ax³+2bx²-cx-4d,即bx²-2d=0恒成立 ∴b=0，d=0∴f（x）=ax³+cx，f'（x）3ax²+c， ∵x=1时，f（x）取极小值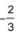，∴3a+c=0且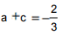，解得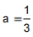，c=-1 （2）当x∈[-1，1]时，图象上不存在这样的两点使结论成立. 假设图象上存在两点A（x₁，y₁）、B（x₂，y₂），使得过此两点处的切线互相垂直， 则由f’（x)=x²-1，知两点处的切线斜率分别为k₁=x₁²-1.k₂=x₂²-1， 且（x₁²-1）（x₂²-1）=-1…（*） ∵x₁、x₂∈[-1，1]，∴x₁²-1≤0，x₂²-1≤0，∴（x₁²-1）（x₂²-1）≥0 此与（*）相矛盾，故假设不成立. 证明（3）∵f（x）=x²-1，令f’（x）=0.得x=±1，x∈（-∞,-1）， 或x∈（1,+∞）时，f’（x)＞0;x∈（-1.1）时，f’（x)＜0， ∴f（x）在[-1，1]上是减函数，且 ∴在[-1，1]上，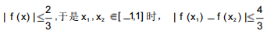

填空题

1、盒中有3个白球和5个红球，任意取出一个球，取出的是红球的概率为_______  

答 案：p=5/8

2、若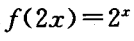，则f(8)=_____。  

答 案：16