2025年高职单招《数学》每日一练试题11月18日

2025年高职单招《数学》每日一练试题11月18日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、某人参加射击比赛，一次射击命中的环数为{偶数环}是随机事件。（）  

答 案：对

解 析：在随机试验中，可能出现也可能不出现，而在大量重复试验中具有某种规律性的事件叫做随机事件

2、0属于空集。（）  

答 案：错

解 析：0不是空集，含有元素0，所以不是空集。

单选题

1、用1，2，3，4四个数字组成恰有两个相同数字的四位偶数的个数是()  

• A：72个
• B：36个
• C：144个
• D：108个

答 案：A

2、函数f(x)=4x-2的零点是()  

• A：X=1/2
• B：X=0
• C：X=1
• D：X=2

答 案：A

解 析：f(x)=4x-2，当x等于0时，x=1/2，故选A。

多选题

1、已知等差数列{a_n}的前n项和为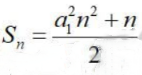，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：
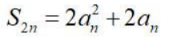
• D：2S_n-a_n=1+3+5+...+(2n-1)

答 案：ABD

2、已知函数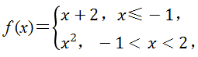关于函数f(x)的结论正确的是(　　)  

• A：f(x)的值域为(－∞，4)
• B：f(1)＝3
• C：若f(x)＝3，则x的值是
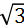
• D：f(x)<1的解集为(－1，1)

答 案：AC

解 析：当x≤－1时，f(x)的取值范围是(－∞，1]，当－1＜x＜2时，f(x)的取值范围是[0，4)，因此f(x)的值域为(－∞，4)，故A正确；当x＝1时，f(1)＝12＝1，故B错误；当x≤－1时，由x＋2＝3，解得x＝1(舍去)，当－1＜x＜2时，由x2＝3，解得x＝或x＝－(舍去)，故C正确；当x≤－1时，由x＋2＜1，解得x＜－1，当－1＜x＜2时，由x²＜1，解得－1＜x＜1，因此f(x)＜1的解集为(－∞，－1)∪(－1，1)，故D错误.故选AC.

主观题

1、已知函数f(x)=(ax+b)lnx. (1)当a=1,b=0时，求函数y=f(x)的极值； (2)当a=1,b=1时，求不等式f(x)≥2x-2的解集； (3)当a=1,b=1时，若当x∈(1,+∞),恒有f(x)＞λ(x-1)成立，求实数λ的取值范围.

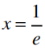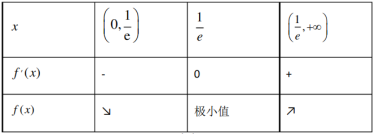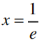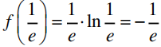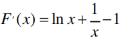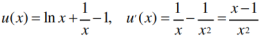答 案：(1)当a=1,b=0,f(x)=xlnx,f'(x)=1+lnx,定义域(0,+∞) 令f'(x)=1+lnx=0,得. 列表如下： ∴当时，f(x)有极小值，无极大值； (2)当a=1,b=1,f(x)=(x+1)·lnx 令F(x)=f(x)-(2x-2)=(x+1)·lnx-(2x-2) 令 列表如下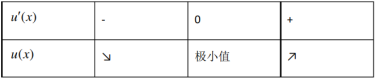： 当x=1时，u(x)有极小值u(1)=ln1+1-1=0∴u(x)≥0,即F'(x)≥0 ∴F(x)在(0,+∞)单调递增，F(1)=0,故不等式f(x)≥2x-2即F(x)≥0=F(1),故解集为[1,+∞)； (3)当a=1,b=1,f(x)=(x+1)·lnx,当x∈(1,+∞),恒有f(x)＞λ(x-1)成立，即x∈(1,+∞),恒有f(x)-λ(x-1)＞0成立. 令G(x)=f(x)-λ(x-1)=(x+1)lnx-λ(x-1) 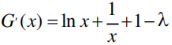令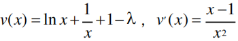 x∈(1,+∞),∴v’(x)＞0,∴v(x)在(1,+∞)单调递增，∴v(x)＞v(1)=2-λ ①若2-λ≥0,即λ≤2,v(x)＞0,即G'(x)＞0,即G(x)在(1,+∞)单调递增. ∵x∈(1,+∞)∴G(x)＞G(1)=0成立. 即λ≤2时，当x∈(1,+∞),恒有f(x)＞λ(x-1)成立. ②若2-λ＜0,即λ＞2,取x=e^λ＞1 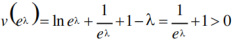V(x)在(1，+∞)单调递增,∴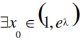，使得v(x₀)=0, ∵当x∈(1,x₀)，v(x)＜0,即G'(x)＜0, ∴G(x)在(1,x₀)上单调递减∵G(x₀)＜G(1)=0, ∴当x∈(1,+∞)时，G(x)＞0不恒成立，即f(x)＞λ(x-1)不恒成立. 综上：λ≤2.

2、设t≠0，点P（t，0）是函数f（x)=x³+ax与g（x）=bx²+c的图象的一个公共点，两函数的图象在点P处有相同的切线 （I）用t表示a，b，c； （II）若函数y=f（x)-g（x）在（-1，3）上单调递减，求t的取值范围.

答 案：（1）因为函数f（x），g（x）的图象都过点（t，0），所以f（t）=0，即t³+at=0.因为t≠0,所以a=-t².g（t）=0.即bt²+c=0.所以c=ab 又因为f（x），g（x）在点（t，0）处有相同的切线，所以f’(t)=g’(t) 而f’（x)=3x²+a，g’（x)=2bx，所以3t²+a=2bt. 将a=-t²代入上式得b=t.因此c=ab=-t³.故a=-t²，b=t，c=-t³ （Ⅱ）解法一：y=f（x)-g（x)=x³-t²x-tx²+t³，y'=3x²-2tx-t²=（3x+t）（x-t). 当y’=（3x+t)（x-t)＜0时，函数y=f（x)-g（x)单调递减. 由y'＜0，若t＞0，则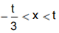；若t＜0.则 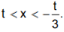由题意，函数y=f（x)-g（x)在（-1，3）上单调递减，则.所以t≥3或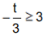.即t≤-9或t≥3. 又当-9＜t＜3时，函数y=f（x)-g（x)在（-1，3）上单调递减. 所以t的取值范围为（-∞，-9]∪[3，+∞）. 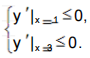解法二：y=f（x)-g（x)=x³-t²x-tx²+t³，y’=3x²-2tx-t²=(3x+t)(x-t) 因为函数y=f（x)-g（x）在（-1，3）上单调递减，且y'=（3x+t）（x-t）是（-1，3）上的抛物线，所以即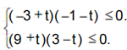解得t≤-9或t≥3. 所以t的取值范围为（-∞，-9]∪[3.+∞）

填空题

1、抛物线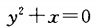的焦点坐标是_______，准线方程是_______.

答 案：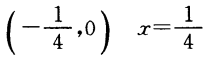

2、函数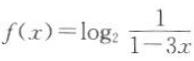的定义域为（）.

答 案：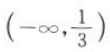

解 析：要使f(x)有意义，须满足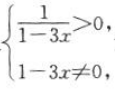解得