2025年高职单招《数学》每日一练试题11月17日

2025年高职单招《数学》每日一练试题11月17日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、一辆大货车和一辆小轿车同时从A城出发开往B城，大货车每时行驶75千米，小轿车每时行驶80千米，两车4小时后相距15千米。（）  

答 案：错

解 析：首先用小轿车的速度减去大货车的速度，求出两车的速度之差是多少；然后根据路程÷速度=时间，用15除以两车的速度之差，求出几小时后两车相距15千米即可。解：15÷（80-75）=15÷5=3（小时），答：3小时后两车相距15千米。

2、函数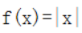与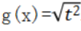表示同一个函数。（）  

答 案：对

解 析：f(x)=|x|和g(x)=根号下是同一函数.
因为它们的定义域相同,都是R.
它们的对应规律相同,即自变量的绝对值等于函数值.
函数的两个要素均相同.
所以,它们是同一函数.
此外,它们的图象完全重合.
注意两点：
1.函数关系（特别提示：仅仅指函数关系）与表示自变量和函数的字母无关.
2.当我们比较两个函数关系异同的时候,往往是先化简,再比较.
如函数y＝x/x与u＝t⁰,分别化简为y＝1,且x≠0；u＝1,t≠0.按上述考察,它们是同一函数.
从形式上看,前者是分式函数,后者是幂函数.
“形式”是入门的向导,入门以后应抓住“本质”.
化简以后,也就是把它们的面纱揭去以后,原来它们是同一个函数.
最后,f(x)=|x|和g(x)=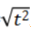不是同一函数.特别注意后者g(x)明明白白表示g是自变量x的函数.而根号下中是否含有x,不得而知.

单选题

1、已知点M（1,6），N（7,3），则直线MN的斜率为（）  

• A：-2
• B：-1/2
• C：1/2
• D：2

答 案：B

2、（）  

• A：
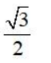
• B：
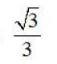
• C：
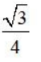
• D：

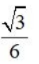
答 案：D

多选题

1、当函数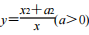在 x＝x₀处的导数为 0 时，那么 x₀可以是( )  

• A：a
• B：0
• C：-a
• D：a²

答 案：AC

解 析：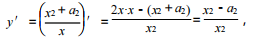

2、下列四个命题中正确的是（）  

• A：与圆有公共点的直线是该圆的切线
• B：垂直于圆的半径的直线是该圆的切线
• C：到圆心的距离等于半径的直线是该圆的切线
• D：过圆直径的端点，垂直于此直径的直线是该圆的切线

答 案：CD

解 析：A中，与圆有两个公共点的直线，是圆的割线，故该选项不符合题意；B中，应经过此半径的外端，故该选项不符合题意；C中，根据切线的判定方法，故该选项符合题意；D中，根据切线的判定方法，故该选项符合题意。故选：CD。

主观题

1、已知函数f（x）＝ae^x﹣lnx﹣1． （1）设x＝2是f（x）的极值点，求a，并求f（x）的单调区间； （2）证明：当a≥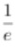时，f（x）≥0．

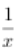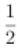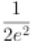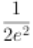答 案：解：（1）∵函数f（x）=ae^x-lnx-1． ∴x＞0，f′（x）=ae^x-， ∵x=2是f（x）的极值点， ∴f′（2）=ae²-=0，解得a=， ∴f（x）=e^x-lnx-1， ∴f′（x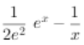）=，显然f′（x）在（0，+∞）上单调递增， ∴当0＜x＜2时，f′（x）＜0，当x＞2时，f′（x）＞0， ∴f（x）在（0，2）单调递减，在（2，+∞）单调递增． （2）证明：当a≥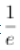时，f（x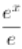）≥-lnx-1， 设g（x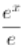）=-lnx-1，则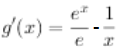， 由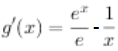=0，得x=1，且g’(x)在（0，+∞）上单调递增， 当0＜x＜1时，g′（x）＜0， 当x＞1时，g′（x）＞0， ∴x=1是g（x）的极小值点，也是最小值点， 故当x＞0时，g（x）≥g（1）=0， ∴当a≥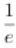时，f（x）≥0．

2、已知函数f(x)=(ax+b)lnx. (1)当a=1,b=0时，求函数y=f(x)的极值； (2)当a=1,b=1时，求不等式f(x)≥2x-2的解集； (3)当a=1,b=1时，若当x∈(1,+∞),恒有f(x)＞λ(x-1)成立，求实数λ的取值范围.

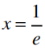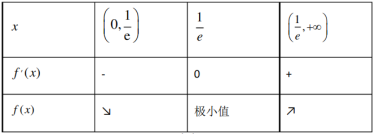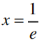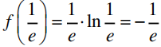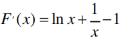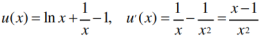答 案：(1)当a=1,b=0,f(x)=xlnx,f'(x)=1+lnx,定义域(0,+∞) 令f'(x)=1+lnx=0,得. 列表如下： ∴当时，f(x)有极小值，无极大值； (2)当a=1,b=1,f(x)=(x+1)·lnx 令F(x)=f(x)-(2x-2)=(x+1)·lnx-(2x-2) 令 列表如下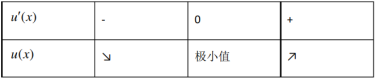： 当x=1时，u(x)有极小值u(1)=ln1+1-1=0∴u(x)≥0,即F'(x)≥0 ∴F(x)在(0,+∞)单调递增，F(1)=0,故不等式f(x)≥2x-2即F(x)≥0=F(1),故解集为[1,+∞)； (3)当a=1,b=1,f(x)=(x+1)·lnx,当x∈(1,+∞),恒有f(x)＞λ(x-1)成立，即x∈(1,+∞),恒有f(x)-λ(x-1)＞0成立. 令G(x)=f(x)-λ(x-1)=(x+1)lnx-λ(x-1) 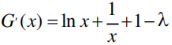令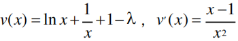 x∈(1,+∞),∴v’(x)＞0,∴v(x)在(1,+∞)单调递增，∴v(x)＞v(1)=2-λ ①若2-λ≥0,即λ≤2,v(x)＞0,即G'(x)＞0,即G(x)在(1,+∞)单调递增. ∵x∈(1,+∞)∴G(x)＞G(1)=0成立. 即λ≤2时，当x∈(1,+∞),恒有f(x)＞λ(x-1)成立. ②若2-λ＜0,即λ＞2,取x=e^λ＞1 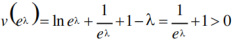V(x)在(1，+∞)单调递增,∴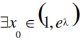，使得v(x₀)=0, ∵当x∈(1,x₀)，v(x)＜0,即G'(x)＜0, ∴G(x)在(1,x₀)上单调递减∵G(x₀)＜G(1)=0, ∴当x∈(1,+∞)时，G(x)＞0不恒成立，即f(x)＞λ(x-1)不恒成立. 综上：λ≤2.

填空题

1、已知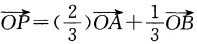，则  

答 案：1/3

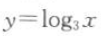2、函数与函数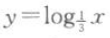的图像关于（）对称.

答 案：x轴

解 析：因为,所以两个函数图像关于x轴对称.