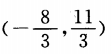2025年高职单招《数学》每日一练试题11月14日

2025年高职单招《数学》每日一练试题11月14日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、三点确定一个平面。（）  

答 案：错

解 析：三点确定一个平面，显然不正确，当三点共线，不能确定一个平面．

2、设集合A={a,b,c},B={c,d},则AUB={a,b,c,d}。（）  

答 案：对

解 析：AUB为集合A和集合B合并到一起

单选题

1、若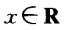，则下列不等式中恒成立的是（）

• A：
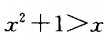
• B：
• C：
• D：

答 案：A

2、吗某机械厂2016年的产值为100万元，预计每年以5％的幅度递增，则该厂到2020年的预计产值（万元）是（）  

• A：
• B：
• C：
• D：

答 案：C

多选题

1、已知函数 f(x)的定义域为 R,其导函数 f'(x)的图象如图所示,则对于任意 x 1 ,x2∈R(x1≠x 2 ),下列结论正确的是( )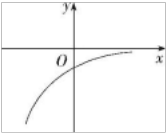  

• A：(x1 -x2 )[f(x1 )-f(x2 )]<0
• B：(x1 -x2 )[f(x1 )-f(x2 )]>0
• C：
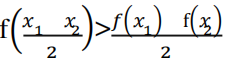
• D：

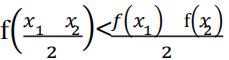
答 案：AD

解 析：由题中图象可知,导函数 f'(x)的图象在 x 轴下方,即 f'(x)<0,且其绝对值越来越小,因此过函数 f(x)图象上任一点的切线的斜率为负,并且从左到右切线的倾斜角是越来越大的钝角,由此可得 f(x)的大致图象如图所示.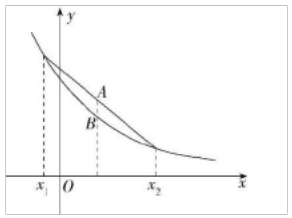 A 选项表示 x 1 -x₂与 f(x₁ )-f(x₂ )异号,即 f(x)图象的割线斜率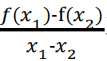为负，故 A 正确;B 选项表示 x ₁ -x₂与 f(x₁ )-f(x₂ )同号,即 f(x) 图象的割线斜率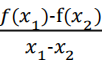为正,故 B 不正确; 对应的函数值,即图中点 B 的纵坐标时所对应的函数值的平均值,即图中点 A 的纵坐标,显然有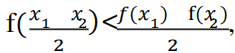 故 C 不正确,D 正确.故选 AD.  

2、函数 y=cos（2x+1）的导数是（）  

• A：y′=sin（2x+1）
• B：y′=—2xsin（2x+1）
• C：y′=—2sin（2x+1）
• D：y′=2xsin（2x+1）

答 案：C

解 析：函数的导数 y′=—sin（2x+1）（2x+1）′=—2sin（2x+1）， 故选：C

主观题

1、已知函数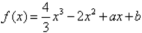的图像在点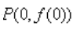处的切线方程为y=2x+1. （Ⅰ）求实数a,b 的值； （Ⅱ）设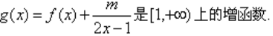. （ⅰ）求实数的最大值； （ⅱ）当m取最大值时，是否存在点Q ，使得过点Q的直线能与曲线y=g(x)围成两个封闭图形，则这两个封闭图形的面积总相等？若存在，求出点Q的坐标；若不存在，说明理由.

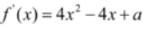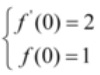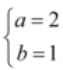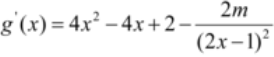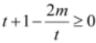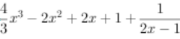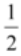答 案：解：（Ⅰ）由及题设得即. （Ⅱ）（ⅰ）由 （Ⅰ）得 , ∵ g(x)是上的增函数， ∴g’(x)≥0在  上恒成立, 即 在上恒成立. 设(2x-1)²=t  ,则t∈[1,+∞） , 即不等式在t∈[1,+∞）上恒成立, 所以2m≤t²+t在[1,+∞）上恒成立. 令y=t²+t，t∈[1,+∞），可得y_min=2，故m的最大值为1 . （ⅱ）由（ⅰ）得  ，g(x)=, 将函数g(x)的图像向左平移个长度单位，再向下平移个长度单位，所得图像相应的函数解析式为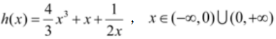 . 由于h(-x)=-h(x)， 所以h(x)为奇函数，故h(x) 的图像关于坐标原点成中心对称.  由此即得，函数g(x)的图像关于点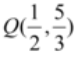成中心对称. 这也表明，存在点，是得过点Q的直线若能与函数g(x)的图像围成两个封闭图形，则这两个封闭图形的面积总相等.

2、已知函数f(x)=xlnx,g(x)=x²+ax(a∈R) (1)设f(x)图象在点(1,0)处的切线与g(x)的图象相切，求a的值； (2)若函数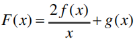存在两个极值点x₁,x₂,且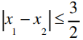,求F(x₁)-F(x₂)的最大值.  

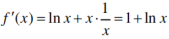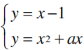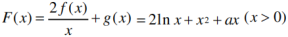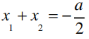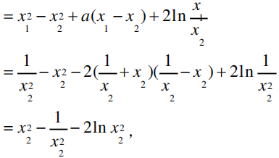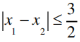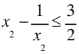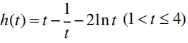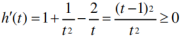答 案：(1)f(x)=xlnx, 所以f(x)图象在点(1,0)处的切线的斜率为f'(1)=1, 所以f(x)图象在点(1,0)处的切线方程为y=x-1, 联立,消去y并整理得x²+(a-1)x+1=0, 依题意可得△=(a-1)²-4=0,解得a=3或-1. (2), 依题意可得x₁,x₂是F'(x)=0,即2x²+ax+2=0的两个正实根， 所以,x₁x₂=1, 不妨设0＜x₁＜1＜x₂,则当x₁＜x＜x₂时，2x²+ax+2＜0,则F'(x)＜0,F(x)在(x₁,x₂)上单调递减，则F(x₁)＞F(x₂), 所以|F(x₁)-F(x₂)|=F(x₁)-F(x₂)=21nx₁+x₁²+ax₁-21nx₂-x₂²-ax₂ 令t=x₂²,则t>1, 又，所以，即2x₂²-3x₂-2≤0,解得1＜x₂≤2，所以1＜t≤4, 设，则， 所以h(t)在[1,4]上单调递增，所以当t=4时，h(t)取得最大值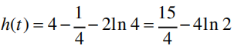即F(x₁)-F(x₂)的最大值为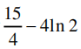

填空题

1、设Sn,是等差数列{an}的前n项和，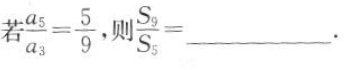  

答 案：1

解 析：由等差数列的性质，可得a₁+a₉=2a₅,a₁+a₅=2a₃,所以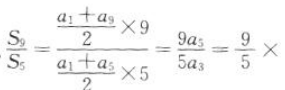

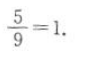
2、平面上A（-2，1），B（1，4），D（4，-3），C点满足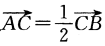，连接DC并延长至E，使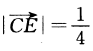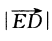，则点E坐标为________  

答 案：