2025年高职单招《数学(中职)》每日一练试题09月26日
2025-09-26 15:51:53 来源:勒克斯教育网
2025年高职单招《数学(中职)》每日一练试题09月26日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、直线x-y+2=0被圆(x-2)2+(y-3)2=1所截得的弦长为()
- A:1
- B:

- C:

- D:3
答 案:C
解 析:由圆(x-2)²+(y-3)²=1可知圆心的坐标为(2,3),半径r=1.因为圆心(2,3)到直线x-y+2=0的距离 ,所以所求弦长为
,所以所求弦长为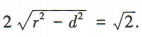 。
。
2、为了得到y=2sinx的图像,只需把函数y=sinx图像上的所有点的()
- A:横坐标缩短到原来的
 纵坐标不变
纵坐标不变 - B:横坐标伸长到原来的2倍,纵坐标不变
- C:纵坐标缩短到原来的
 ,横坐标不变
,横坐标不变 - D:纵坐标伸长到原来的2倍,横坐标不变
答 案:D
解 析:易知将函数y=sinx图像上的所有点的纵坐标伸长到原来的2倍,横坐标不变,可得到函数y=2sinx的图像.
3、设m,n为两条不同的直线,α,β为两个不同的平面,则下列说法正确的是( ).
- A:若m⊥n,n//α,则m//α
- B:若m//n,m//α,n//β,则α//β
- C:若α⊥β,m⊂α,n⊂β,则m⊥n
- D:若m⊥n,m⊥α,n⊥β,则α⊥β
答 案:D
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、如图,在长方体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=2,则二面角A-DD1-B的正切值为()

答 案: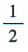
解 析:易得 ,
, 平面角.在
平面角.在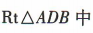 ,AB=1AD=2,
,AB=1AD=2,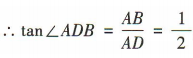 ,∴二面角A-DD1-B的正切值为
,∴二面角A-DD1-B的正切值为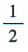 .
.
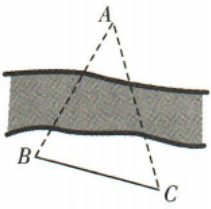
2、如图,A,B两点在河的两岸,在B同侧的河岸边选取点C,测得BC的距离为10,∠ABC=75°,∠ACB=60°,则A,B两点间的距离为()
答 案: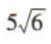
解 析:
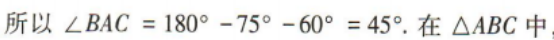
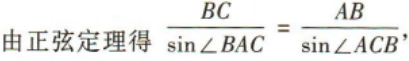
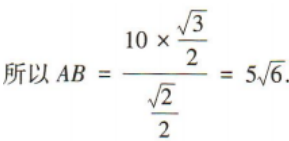
3、已知抛物线的方程为y2=8x,则抛物线的焦点到准线的距离是()
答 案:4
解 析:因为抛物线的方程为y2=2px=8x,所以抛物线的焦点到准线的距离p=4.
简答题
1、已知双曲线C的标准方程为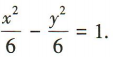 (1)求双曲线C的离心率,左、右焦点F1,F2的坐标;
(2)若点M(3,m)在双曲线C上,证明:
(1)求双曲线C的离心率,左、右焦点F1,F2的坐标;
(2)若点M(3,m)在双曲线C上,证明: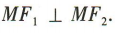
答 案:(1)由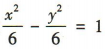 ,可得
,可得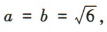 所以
所以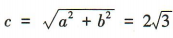 ,离心率
,离心率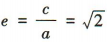 ,左、右焦点的坐标分别为
,左、右焦点的坐标分别为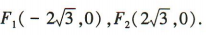 (2)因为点M(3,m)在双曲线C上,
所以
(2)因为点M(3,m)在双曲线C上,
所以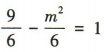 ,解得m2=3,
所以直线 MF1的斜率
,解得m2=3,
所以直线 MF1的斜率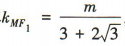 ,直线MF2的斜率
,直线MF2的斜率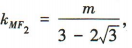 因为
因为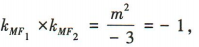 所以
所以