2025年高职单招《数学》每日一练试题09月24日

2025年高职单招《数学》每日一练试题09月24日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、平面向量的加法运算只遵循平行四边形法则（）  

答 案：错

解 析：平面向量的加法运算有三角形法则和平行四边形法则，题目中说“只遵守”不对。

2、正方体不仅相对的面的面积相等，而且所有相邻的面的面积也都相等。（）  

答 案：对

解 析：正方体有6个面，每个面都是面积相等的正方形，所以，正方体不仅相对的面的面积相等，而且所有相邻的面的面积也都相等

单选题

1、在Rt△ABC中，∠C＝90°，各边都扩大2倍，则锐角A的锐角三角函数值()  

• A：扩大2倍
• B：缩小1/2
• C：不变
• D：无法确定

答 案：C

2、甲，乙，丙三个车间生产的某种产品的件数分别为120，80，60现采用分层抽样的方法从中抽取一个容量为n的样本，若从乙车间生存的产品中抽取4件，则n=（）  

• A：10
• B：12
• C：13
• D：14

答 案：C

解 析：注意分层抽样法是按照一定比例抽取样本，因为乙车间是4件，所以抽取比例是1/20，所以n=（120+80+60）*（1/20）

多选题

1、下列关系式正确的是（）  

• A：
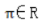
• B：-5∈Z
• C：
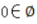
• D：1/2∈Q

答 案：ABD

解 析：A：R是实数，为有理数和无理数。B：在数学里用大写符号Z表示全体整数的集合，包括正整数、0、负整数。D：Q是有理数的集合。C：空集是没有任何元素的，因此也不会有元素0，因此C选项错误，ABD正确。

2、已知数列{3n-1}，下面选项正确的是（）  

• A：这个数列是公比为3的等比数列
• B：这个数列是公差为3的等差数列
• C：这个数列的第5项是14
• D：20是这个数列的第7项

答 案：BCD

解 析：已知数列{3n-1}，这个数列是公差为3的等差数列，故A错误，B正确。数列第五项=3*5-1=14。故C正确。数列第七项=3*7-1=20.故D正确

主观题

1、甲、乙两支球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束.除第五局甲队获胜的概率是外，其余每局比赛甲队获胜的概率都是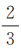.假设各局比赛结果相互独立. (1)分别求甲队以3:0,3:1,3:2获得比赛胜利的概率； (2)若比赛结果为3:0或3:1,则胜利方得3分，对方得0分；若比赛结果为3:2,则胜利方得2分，对方得1分.求乙队得分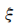的分布列和数学期望.  

答 案：（1）设“甲队以3:0胜利”为事件A，“甲队以3:1胜利”为事件B，“甲队以3:2胜利”为事件C，则 （2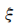）的所有可能取值为0,1,2,3,设“乙队以3:2胜利”为事件D，由于各局比赛结果相互独立， 则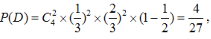 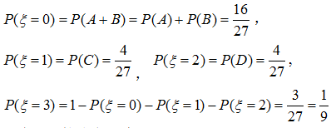因此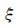，的分布列为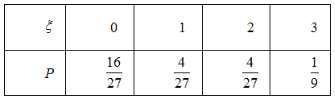 的数学期望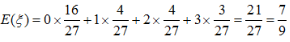  

2、某投资商计划用60万元投资甲、乙两个项目.根据预判，甲项目最大亏损率为20%,乙项目最大亏损率为30%,最大亏损不能超过16万元；甲、乙两个项目的最大盈利率分别为70%和60%.问投资商对甲、乙两个项目分别投资多少万元时，才能使盈利最大?最大盈利是多少万元?  

答 案：设投资商对甲、乙两个项目分别投资x,y万元，获得的盈利为z万元，则有 目标函数z=0.7x+0.6y, 作可行域，如图所示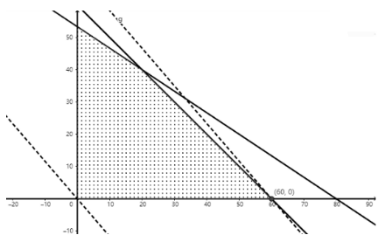： 作0等值线l₀：0.7x+0.6y=0，并平移0等值线，当直线l₀经过可行域中的点（60，0）时，目标函数z取到最大值 所以，当x=60，y=0时，最大盈利为0.7×60+0.6×0=42（万元） 因此，投资商对甲、乙两个项目分别投资60万元和0万元才能使盈利最大，最大盈利为42万元

填空题

1、观察下列图形的排列规律（其中△是三角形，口是正方形，〇是圆)，口△O口口△O口口△O口口△O……若第一个图形是正方形，则第2006个图形是______(填图形名称)  

答 案：三角形

解 析：观察图形的排列规律知，4个图形循环一次，2006÷4=501…2，又由第一个图形是正方形，则第2006个图形是三角形。故答案为：三角形

2、集合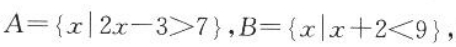则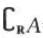∩B=（）.

答 案：(-∞,5]

解 析：根据题意解得集合A=(x|x>5),B=(x|x<7),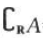=(x|x≤5),所以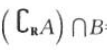=(-∞,5].