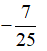2025年高职单招《数学》每日一练试题09月13日

2025年高职单招《数学》每日一练试题09月13日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、在同一平面内，过一点有且只有一条直线与已知直线垂直。（）  

答 案：对

解 析：根据垂线的性质:平面内,过一点有且只有一条直线与已知直线垂直

2、一名学生在七次数学测验中所得分数分别为85,82,86,82,91,86,82,则此学生所得分数的众数是86。()  

答 案：错

解 析：在这一组数据中82是出现次数最多的，故众数是82。

单选题

1、函数的定义域为（）  

• A：（-2，1）
• B：[-2，1]
• C：（-2，+∞）
• D：（-2，1]

答 案：D

解 析：根号下有意义的定义域为≥0的实数,所以x≤1；lg函数的定义域为>0，所以x+2＞0，所以x＞-2，两个定义域的区间为D

2、实数lg4+2lg5的值为()  

• A：2
• B：5
• C：10
• D：20

答 案：A

多选题

1、已知点P到圆O上的点的最大距离是7cm，最小距离是1m，则圆O的半径是（）  

• A：4cm
• B：3cm
• C：5cm
• D：6cm

答 案：AB

2、设等差数列{a_n}的公差为d，其前n项和为S_n，且a₁=-5，S₃=-9，则（）  

• A：d=2
• B：S₂，S₄，S₆为等差数列
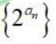• C：数列是等比数列
• D：S₃是S_n的最小值

答 案：ACD

主观题

1、如图所示，在平面四边形ABCD中，AB=√5,AC=3,BC=2√2. 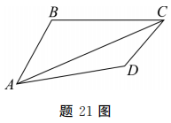(1)求∠ACB的大小； (2)若cos∠ADC=,cos∠BCD=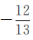,求线段AD的长.  

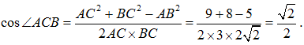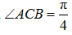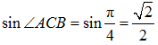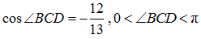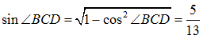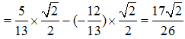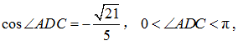答 案：（1）在△ABC中，由余弦定理得 因为0＜∠ACB＜π，所以 （2）由（1）可知 因为，所以 Sin∠ACD=sin(∠BCD-∠ACB)=sin∠BCDcos∠ACB-cos∠BCDsin∠ACB 又因为 所以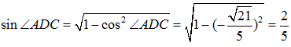 在△ACD中，由正弦定理得 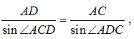所以  

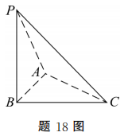
2、如图所示，在三棱锥P-ABC中，PB⊥平面ABC,AB⊥AC,垂足为点A (1)证明：AC⊥平面PAB; (2)若AC=3,BC=√10,直线PC与平面PAB所成的角为30°,求三棱锥B-PAC的体积.  

答 案：（1）证明：因为PB⊥平面ABC，AC⊆平面ABC，所以PB⊥AC 又因为AB⊥AC，AB,PB⊆平面PAB，AB∩PB=B, 所以AC⊥平面PAB （2）因为直线PC与平面PAB所成的角为30°，AC⊥平面PAB， 所以在直角三角形PAC中，∠CPA=30°,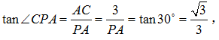 解得PA=3√3 又因为△ABC的面积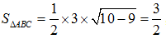，PB⊥平面ABC 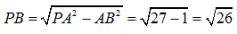所以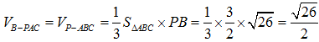  

填空题

1、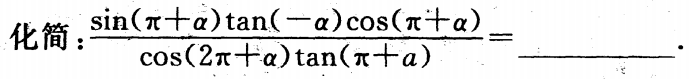  

答 案：-sina

2、已知角α的顶点在坐标原点,始边与x轴的非负半轴重合,终边上一点的坐标为(6,-8),则cos2α=（）.

答 案：