2025年成考专升本《高等数学二》每日一练试题10月18日

2025年成考专升本《高等数学二》每日一练试题10月18日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、若，则。（）  

答 案：错

解 析：

单选题

1、下列说法正确的是（）.

• A：如果A、B是互斥事件，则P（A）＋P（B）＝1
• B：若P（A）＋P（B）＝1，则A、B必定是互斥事件
• C：如果A、B是对立事件，则P（A）＋P（B）＝1
• D：若P（A）＋P（B）＝1，则事件A与B是对立事件

答 案：C

解 析：AC两项，事件A和B的交集为空集，A与B就是互斥事件，也叫互不相容事件，其中必有一个发生的两个互斥事件叫做对立事件，若A，B是对立事件，则P（A）＋P（B）＝1；BD两项，互斥事件和对立事件的前提的是A与B事件的交集为空集，虽然P（A）＋P（B）＝1，但不能保证A与B事件的交集为空集.

2、（）。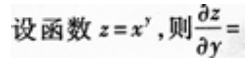  

• A：x^y
• B：x^ylny
• C：x^ylnx
• D：y^xy-1

答 案：C

主观题

1、己知某篮球运动员每次投篮投中的概率是0.9，记X为他两次独立投篮投中的次数．（1）求X的概率分布；
（2）求X的数学期望EX．

答 案：解：（1）X可能的取值为0，1，2；因此X的概率分布为 （2）数学期望
EX＝0×0.1＋1×0.18＋2×0.81＝1.80

2、某射手击中10环的概率为0.26，击中9环的概率为0.32，击中8环的概率为0.36，求在一次射击中不低于8环的概率．

答 案：解：设A＝{击中10环），B＝{击中9环），C＝{击中8环），D＝{击中不低于8环），则D＝A＋B＋C，由于A，B，C相互独立，所以P（D）＝P（A＋B＋C）＝P（A）＋P（B）＋P（C）＝0.26＋0.32＋0.36＝0.94

填空题

1、设=（）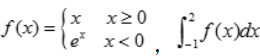  

答 案：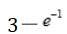

解 析：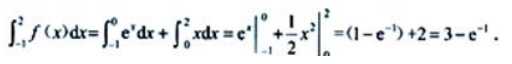

2、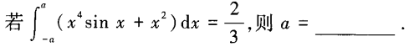  

答 案：1

解 析：被积函数的前一部分是奇函数，后一部分是偶函数，因此有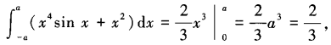： 解得a=1。  

简答题

1、设函数y=ax³+bx+c在点x=1处取得极小值-1，且点（0，1）为该函数曲线的拐点，试求常数a，b，c。  

答 案：本题考查的知识点是可导函数在某一点取得极小值的必要条件以及拐点的概念。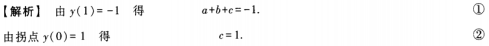  

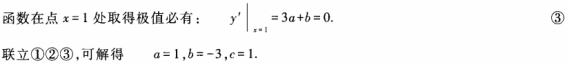
2、设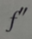存在，

答 案：