2025年成考专升本《高等数学一》每日一练试题06月04日
2025-06-04 11:41:56 来源:勒克斯教育网
2025年成考专升本《高等数学一》每日一练试题06月04日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、下列方程中表示椭球面的是()。
- A:x2+y2-z2=1
- B:x2-y2=0
- C:
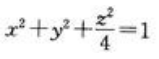
- D:x2+y2=z2
答 案:C
解 析:A项,双曲面的方程为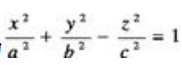 ,所以为双曲面;B项,x2-y2=0表示两条垂直的直线;C项,椭球面的方程为
,所以为双曲面;B项,x2-y2=0表示两条垂直的直线;C项,椭球面的方程为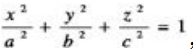 ,符合这一特征;D项,x2+y2=z2表示圆锥体。
,符合这一特征;D项,x2+y2=z2表示圆锥体。
2、微分方程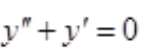 的通解为()。
的通解为()。
- A:y=Ce-x
- B:y=e-x+C
- C:y=C1e-x+C2
- D:y=e-x
答 案:C
解 析:特征方程为r2+r=0,特征根为r1=0,r2=-1;方程的通解为y=C1e-x+C2。
3、设区域D是由直线y=x,x=2,y=1围成的封闭平面图形, ()。
()。
- A:

- B:

- C:

- D:

答 案:D
解 析:积分区域如右图中阴影部分所示。D可以表示为1≤x≤2,1≤y≤x或1≤y≤2,y≤x≤2,对照所给选项,知应选D。 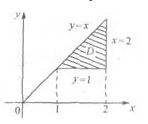
主观题
1、求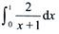 .
.
答 案:解: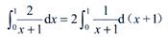
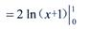 =2ln2
=2ln2
2、设函数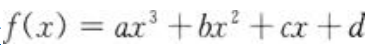 ,问常数a,b,c满足什么关系时,f(x)分别没有极值、可能有一个极值、可能有两个极值?
,问常数a,b,c满足什么关系时,f(x)分别没有极值、可能有一个极值、可能有两个极值?
答 案:解:此函数在定义域(-∞,+∞)处处可导,因此,它的极值点必是驻点即导数等于零的点,求导得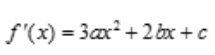 令
令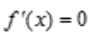 即
即 由一元二次方程根的判别式知:当
由一元二次方程根的判别式知:当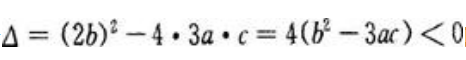 时,
时,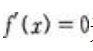 无实根。
无实根。
由此可知,当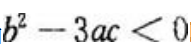 时,f(x)无极值。
时,f(x)无极值。
当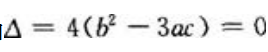 时,
时,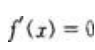 有一个实根。
有一个实根。
由此可知,当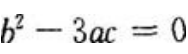 时,f(x)可能有一个极值。
时,f(x)可能有一个极值。
当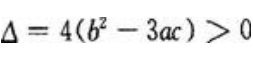 时,f(x)可能有两个极值。
时,f(x)可能有两个极值。
3、求微分方程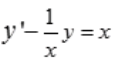 的通解。
的通解。
答 案:解: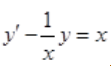 为一阶线性微分方程,则
为一阶线性微分方程,则
填空题
1、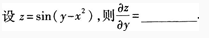
答 案: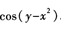
解 析: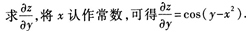
2、设y=3+cosx,则y’=()。
答 案:-sinx。
解 析:本题考查的知识点为导数运算。 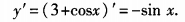
3、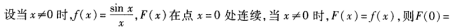 ()。
()。
答 案:1
解 析:本题考查的知识点为函数连续性的概念。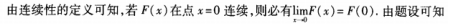
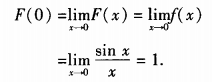
简答题
1、
答 案: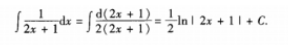
解 析:本题考查的知识点为不定积分运算。 



