2023年成考高起点《数学(理)》每日一练试题01月25日

2023年成考高起点《数学(理)》每日一练试题01月25日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、一位篮球运动员投篮两次，若两投全中得2分，若两投一中得1分，若两投全不中得0分，已知该运动员两投全中的概率为0.375，两投一中的概率为0.5，则他投篮两次得分的期望值是

• A：1.625
• B：1.5
• C：1.325
• D：1.25

答 案：D

2、函数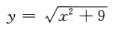的值域为（）。

• A：R
• B：[3,+∞)
• C：[0, +∞)
• D：[9,+ ∞)

答 案：B

解 析：该小题主要考查的知识点为函数的值域.【考试指导】

3、设全集I=｛0,1,2,3,4}，A={0,1,2,3}，B=｛0,3,4}，则是（）。

• A：{2，4}
• B：{1，2}
• C：{0，1｝
• D：{0，1，2，3}

答 案：B

解 析：={0,1,2,3}∩｛1,2}=｛1,2}。

4、下列函数中，在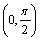为减函数的是（）

• A：y=ln(3x+1)
• B：y=x+1
• C：y=5sinx
• D：y=4-2x

答 案：D

解 析：A、B选项在其定义域上为增函数，选项C在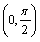上为增函数，只有D选项在实数域上为减函数.

主观题

1、在平面直角坐标系xOy中，已知⊙M的方程为x²+y²-2x+2y-6=0，⊙O经过点M. (Ⅰ）求⊙O的方程； (Ⅱ)证明：直线x-y+2=0与⊙M，⊙O都相切.

答 案：(Ⅰ)⊙M可化为标准方程(x-1)²+(y+1)²=(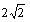)²， 其圆心M点的坐标为（1，-1)，半径为r₁=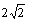， ⊙O的圆心为坐标原点， 可设其标准方程为x²+y²=r₂²， ⊙O过M点，故有r₂=， 因此⊙O的标准方程为x²+y²=2. (Ⅱ)点M到直线的距离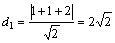， 点O到直线的距离离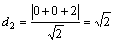， 故⊙M和⊙O的圆心到直线x-y+2=0的距离均等于其半径， 即直线x-y+2=0与⊙M和⊙O都相切.

2、已知等差数列前n项和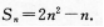
(Ⅰ)求这个数列的逋项公式；
(II)求数列第六项到第十项的和．

答 案：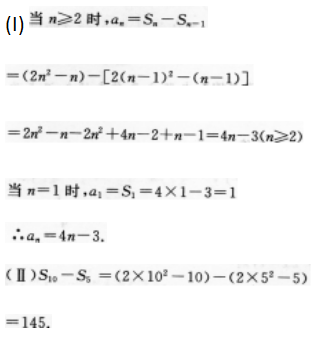

3、

答 案：

4、已知△ABC中，A=30°，AC=BC=1.求(Ⅰ)AB；(Ⅱ)△ABC的面积.

答 案：(Ⅰ)由已知得C=120° 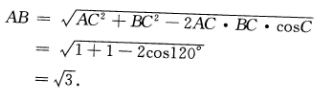(Ⅱ)设CD为AB边上的高，那么 CD=AC·sin30°=1/2 △ABC的面积为

填空题

1、从某大学篮球队历次比赛得分中，抽取了8场比赛的得分作为样本，数据如下：88，74，73，87，70，72，86，90，则该样本的方差为（）。

答 案：62.25

解 析：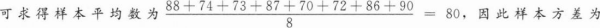

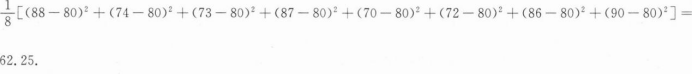
2、设离散型随机变量ζ的分布列如下表所示，那么ζ的期望等于（）。

答 案：89

解 析：E(ξ)=100x0.2+90x0.5+80x0.3=89。