2022年成考高起点《数学(理)》每日一练试题12月30日

2022年成考高起点《数学(理)》每日一练试题12月30日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、

• A：R
• B：
• C：[-3，1]
• D：

答 案：C

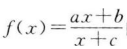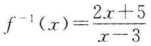2、已知函数的反函数为，则（）。

• A：a=3,b=5，C=2
• B：a=3,b=-2，C=5
• C：a=-3,b=-5，C=2
• D：a=2,b=5，C=-3

答 案：A

解 析：

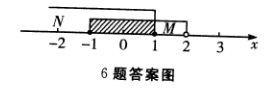
3、设集合M={x∣-1≤x<2}，N={x∣x≤1}集合M∩N=（）。

• A：{x∣-1≤x≤1}
• B：{x∣x>-1}
• C：{x∣1≤x≤2}
• D：{x∣x>1}

答 案：A

解 析：该小题主要考查的知识点为集合之间的关系. 【考试指导】用数轴表示(如图).

4、方程y=-√x的图形是过原点的抛物线，且在（）。

• A：第Ⅰ象限内的部分
• B：第Ⅱ象限内的部分
• C：第Ⅲ象限内的部分
• D：第Ⅳ象限内的部分

答 案：D

解 析：∵顶点在原点的抛物线，开口方向有四种，即向上、向下、向左、向右,向右的可分为两支，一支是y=√x，另一支是y=-√x，由下图可得答案为D。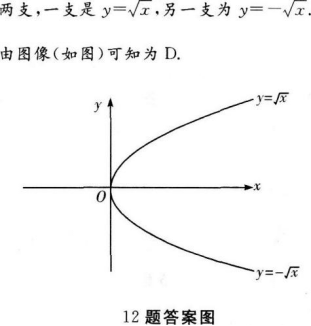

主观题

1、

答 案：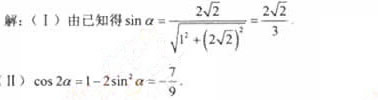

2、已知等差数列前n项和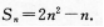
(Ⅰ)求这个数列的逋项公式；
(II)求数列第六项到第十项的和．

答 案：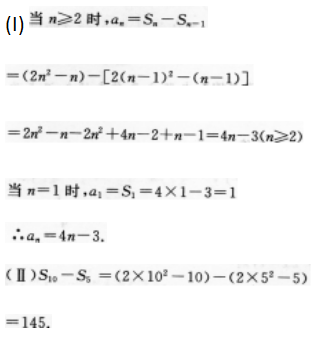

3、已知数列{an}的前n项和 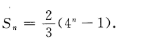(1)求{an}的通项公式; (2)若ak=128，求k。

答 案：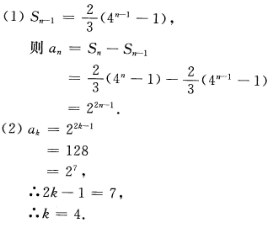

4、已知椭圆C的长轴长为4，两焦点分别为F1(-，0)，F2(，0)。 (1)求C的标准方程;(2)若P为C上一点，|PF1|-|PF2|=2，求cos∠F1PF2。

答 案：

填空题

1、某次测试中5位同学的成绩分别为79,81,85,75,80，则他们成绩的平均数为______.

答 案：80

解 析：该小题主要考查的知识点为平均数. 成绩的平均数=（79+81+85+75+80）/5=80

2、曲线y=x²-e^x+1在点(0，0)处的切线方程为___________________。

答 案：x+y=0  

解 析：本题考查了导数的几何意义的知识点。 根据导数的几何意义，曲线在(0，0)处的切线斜率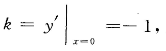，则切线方程为y-0=-1·(x-0)，化简得：x+y=0。