2025年成考高起点《数学(理)》每日一练试题12月13日

2025年成考高起点《数学(理)》每日一练试题12月13日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、棱长等于1的正方体内接于一球体中，则该球的表面积是（）。

• A：6π
• B：
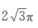
• C：3π
• D：9π

答 案：C

解 析：正方体的大对角线即为内接球的直径,得半径则球的表面积为

2、从1、2、3、4、5、6、7、8、9这九个数字中，随机取出一个数字，这个数字是奇数的概率是（）。

• A：
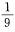
• B：
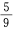
• C：
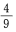
• D：

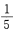
答 案：B

解 析：本题的试验是从1~9这九个数字中任取一个数字，显然选中其中任一个数字的可能 性都是相同的，属于等可能事件的概率，∵n=9，其中奇数个数m=5，∴其概率是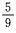，故选B。

3、函数f(x)=x³-6x²+9x-3的单调区间为（）。

• A：(-∞，-3)、(-3，1)、(1，+∞)
• B：(-∞，-1)、(-1，3)、(3，+∞)
• C：(-∞，1)、(1，3)、(3，+∞)
• D：(-∞，-3)、(-3，-1)、(-1，+∞)

答 案：C

解 析：y=x³-6x²+9x-3则y’=3x²+12x+9 令y’=0,x²-4x+3=0（x-1）（x-3）=0解得，x1=1，x2=3 四个答案中，只有C具有1、3两个极值点，其余3个没有，故应选C。  

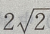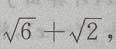
4、在△ABC中，若b=，c=则a等于（）

• A：2
• B：
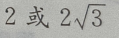
• C：
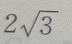
• D：无解

答 案：B

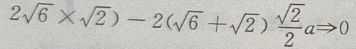
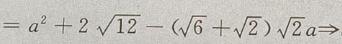
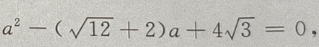解 析：此题是已知两边和其中一边的对角,解三角形时,会出现一解、两解、无解的情况,要注意这一点.用余弦定理可得解出

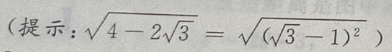
主观题

1、设分别讨论x→0及x→1时f（x）的极限是否存在？

答 案：∴f（x）在x=0处极限不存在 同理f（x）在x=1处极限存在

2、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．

答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得当时，f'(x)时，f'(x)＞O.故f(x）在区间单调递减，在区间单调递增．因此f(x）在时取得极小值

3、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得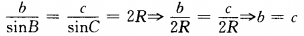

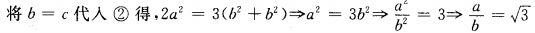
∴a：b=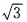：1
于是a：b：c=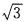：1：1。  

4、在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量和关于基底{a,b,c}的分解式; （Ⅱ）求证： （Ⅲ）求证：  

答 案：（Ⅰ）由题意知(如图所示)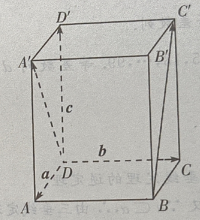  

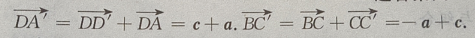
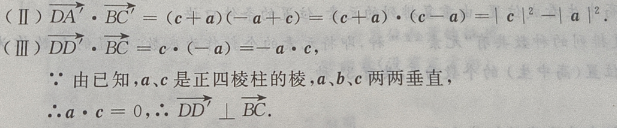
填空题

1、点B（4，-5）按向量a平移后的对应点B0（-4，7），则a的坐标是______。  

答 案：（-8，12）

解 析：由平移公式得-4=4+a1，7=-5+a2→a1=-8，a2=12 ∴a的坐标是（-8，12）。  

2、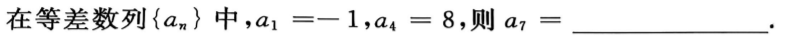

答 案：17

解 析：