2025年成考高起点《数学(文史)》每日一练试题11月14日
2025-11-14 12:22:48 来源:勒克斯教育网
2025年成考高起点《数学(文史)》每日一练试题11月14日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知函数f(x)的定义域为R,且满足f(2x)=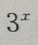 ,则f(x)的反函数为()
,则f(x)的反函数为()
- A:
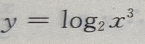
- B:
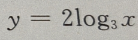
- C:
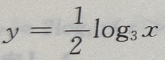
- D:
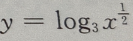
答 案:B
解 析:令2x=t,则x=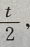
2、设甲:四边形ABCD是平行四边形,乙:四边形ABCD是正方形,则()。
- A:甲是乙的充分条件,但不是乙的必要条件
- B:甲是乙的必要条件,但不是乙的充分条件
- C:甲是乙的充分必要条件
- D:甲不是乙的充分条件,也不是乙的必要条件
答 案:B
3、在△ABC中,三边为a、b、c,∠B=60°,则 的值是()
的值是()
- A:大于零
- B:小于零
- C:等于零
- D:不能确定
答 案:C
解 析:由已知用余弦定理得: 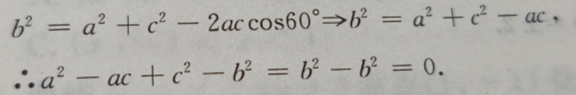
4、设0<x<1,则()。
- A:1<2x<2
- B:0<2x<1
- C:
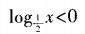
- D:log2x>0
答 案:A
解 析:函数y=2x在区间(-∞,+∞)内为增函数,则2x>20=1,且2x<21=2,选A。
主观题
1、设函数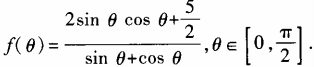 (1)求
(1)求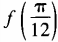 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
2、求证:双曲线的一个焦点到一条渐近线的距离等于虚半轴的长.
答 案:设双曲线的方程为 则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为
则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为 令设焦点F2(c,0)到渐近线
令设焦点F2(c,0)到渐近线 的距离为d,则
的距离为d,则 即从双曲线
即从双曲线 的一个焦点F2(c,0)到一条渐近线
的一个焦点F2(c,0)到一条渐近线 的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线
的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线 以及点F1(-c,0)到渐近线
以及点F1(-c,0)到渐近线 的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
解 析:本题考查的是圆锥曲线与直线位置关系的推理能力,主要是用代数的方法表示几何中的问题.考生必须对曲线方程、几何性质及元素之间的关系有深刻的理解,方可解决此类综合题.这种综合性的圆锥曲线试题出现的概率比较高,要引起重视.
3、
答 案: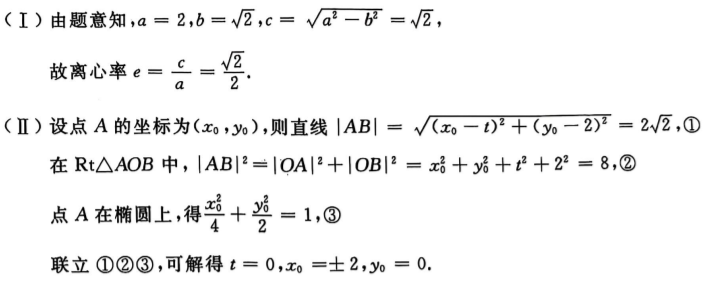
解 析: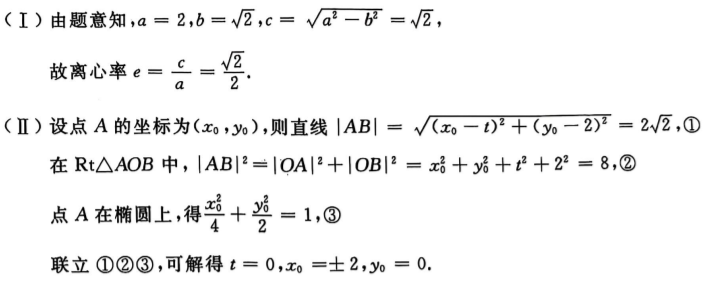
4、已知三角形的一个内角是 ,面积是
,面积是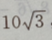 周长是20,求各边的长.
周长是20,求各边的长.
答 案:设三角形三边分别为a,b,c,∠A=60°, 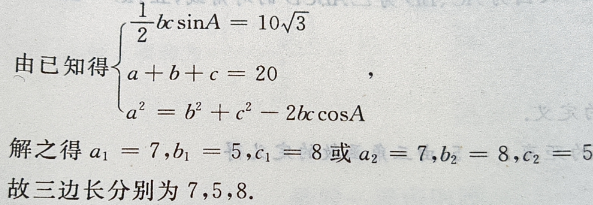
填空题
1、任选一个不大于20的正整数,它恰好是3的整数倍的概率是()
答 案: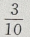
解 析:设n为不大于20的正整数的个数,则n=20,m为在这20个数中3的倍数:3,6、9、12、15、18的个数。 ∴m=6,∴所求概率=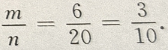
2、5个同学站成一排,其中某个人恰好站在排头的概率是______。
答 案: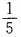
解 析:基本事件的总数n=5!,其中某人恰好站在排头的排法有m=4!种,所求概率为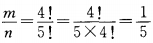 。
。
2022年成考高起点《数学(文史)》每日一练试题11月14日 11-14 2023年成考高起点《数学(文史)》每日一练试题11月14日 11-14 2024年成考高起点《数学(文史)》每日一练试题11月14日 11-14 2025年成考高起点《数学(文史)》每日一练试题04月14日 04-14 2025年成考高起点《数学(文史)》每日一练试题06月14日 06-14 2025年成考高起点《数学(文史)》每日一练试题05月14日 05-14 2025年成考高起点《数学(文史)》每日一练试题03月14日 03-14 2025年成考高起点《数学(文史)》每日一练试题02月14日 02-14



