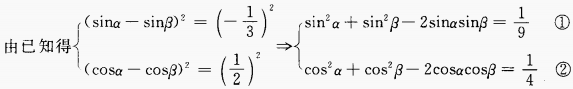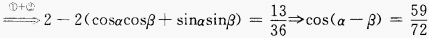2025年成考高起点《数学(理)》每日一练试题11月12日

2025年成考高起点《数学(理)》每日一练试题11月12日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、过A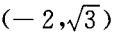B（-5，0）两点直线的倾斜角为（）。

• A：
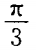
• B：
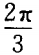
• C：
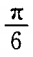
• D：

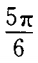
答 案：C

解 析：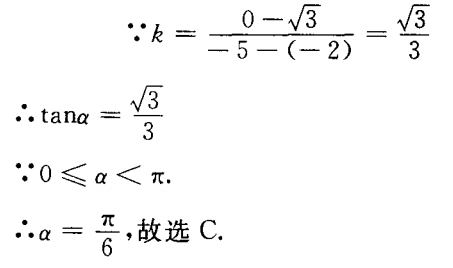

2、下列四个命题中正确的是（）。 ①已知a，b，c三条直线，其中a，b异面，a//c，则b，c异面。
②若a与b异面，b与c异面，则a与c异面。
③过平面外一点与平面内一点的直线，和平面内不经过该点的直线是异面直线。
④不同在任何一个平面内的两条直线叫异面直线。

• A：③④
• B：②③④
• C：①②③④
• D：①②

答 案：A

解 析：①b与c可相交，②a与c可以有平行、相交、异面三种位置关系。答案为A。  

3、曲线y=x+2在点（1，2）处的切线斜率为（）。

• A：1
• B：2
• C：-1
• D：4

答 案：A

解 析：方法一：∵y=x+2，k=y’＝1 方法二：也可用直线方程y=kx+b直接得出k=1。  

4、直线3x-4y-9=0与圆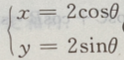(θ为参数)的位置关系是

• A：相交但直线不过圆心
• B：相交但直线通过圆心
• C：相切
• D：相离

答 案：A

解 析：方法一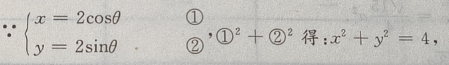： 圆心O（0,0），r=2，则圆心O到直线的距离为 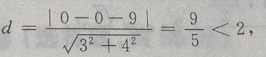0

主观题

1、设（0＜α＜π），求tanα的值。

答 案：

2、已知函数f(x)=(x-4)(x²-a) （I）求f"(x)； (Ⅱ)若f"(-1)=8，求f(x)在区间[0，4]的最大值与最小值

答 案：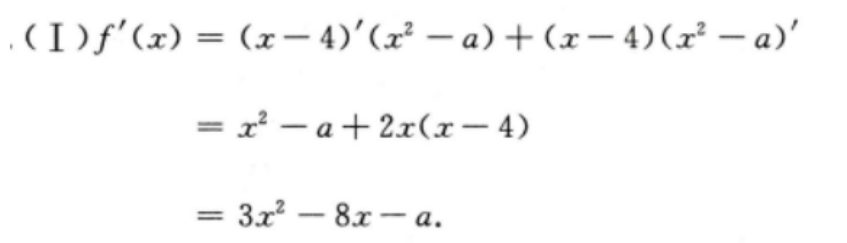

3、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．

答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得当时，f'(x)时，f'(x)＞O.故f(x）在区间单调递减，在区间单调递增．因此f(x）在时取得极小值

4、设分别讨论x→0及x→1时f（x）的极限是否存在？

答 案：∴f（x）在x=0处极限不存在 同理f（x）在x=1处极限存在

填空题

1、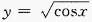的定义域是______。  

答 案：1

解 析：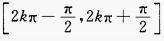

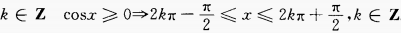
2、已知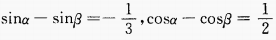，则=______。  

答 案：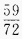

解 析：