2025年成考高起点《数学(文史)》每日一练试题11月07日

2025年成考高起点《数学(文史)》每日一练试题11月07日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若|a|=|b|=1，且a⊥b，又2a+3b与λa-4b互相垂直，则λ为（）

• A：6
• B：-6
• C：3
• D：-3

答 案：A

2、已知b₁、b₂、b₃、b₄成等差数列，且b₁、b₄为方程2x²-3x+1=0的两个根，则b₂+b₃的值为（）。  

• A：1/2
• B：-3/2
• C：-1/2
• D：3/2

答 案：D

3、某车间有甲、乙两台机床，已知甲机床停机的概率为0.06，乙机床停机的概率为0.07，甲、乙两车床同时停机的概率是（）。

• A：0.13
• B：0.0042
• C：0.03
• D：0.04

答 案：B

4、设函数f（x十1)=2x+2，则f(x)=（）

• A：2x-1
• B：2x
• C：2x+1
• D：2x+2

答 案：B

解 析：f（x十1)=2x+2=2(x+1)，令t=x+1，故f(t)=2t，把t换成x，因此f(x)=2x.

主观题

1、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。  

答 案：由已知，得

2、已知a^m=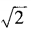，aⁿ=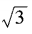，求a^3n-4m的值。  

答 案：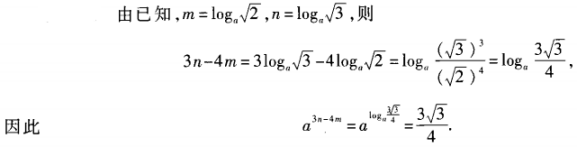

3、设函数f(x)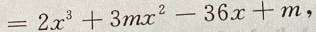且f'(-1)=-36 (Ⅰ)求m (Ⅱ)求f(x)的单调区间

答 案：(Ⅰ)由已知得f'=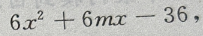 又由f'(-1)=-36得 6-6m-36=-36 故m=1. (Ⅱ)由(Ⅰ)得f'(x)=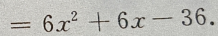 令f'(x)=0，解得 当x<-3时，f'(x)>0; 当-32时，f'(x)>0; 故f(x)的单调递减区间为(-3,2)，f(x)的单调递增区间为(-∞,-3),(2,+∞)  

4、（1）已知tanα=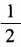 求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1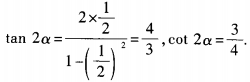） （2）由已知，得 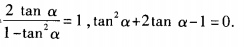解关于tanα的一元二次方程，得tanα=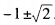

填空题

1、在1000000张奖券中，设有1个一等奖，5个二等奖，10个三等奖，从中买一张奖券，中奖的概率是______。  

答 案：

解 析：本题试验属于等可能事件的概率。n=1000000，m=16，所以买一张奖券，中奖的概率

2、设直线y=2x+m与抛物线y²=4x没有公共点，则m的取值范围是______。  

答 案：