2025年成考高起点《数学(理)》每日一练试题09月29日

2025年成考高起点《数学(理)》每日一练试题09月29日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、给出下列两个命题：①如果一条直线与一个平面垂直，则该直线与该平面内的任意一条直线垂直②以二面角的棱上任意一点为端点，在二面角的两个面内分别作射线，则这两条射线所成的角为该二面角的平面角.则（）

• A：①②都为真命题
• B：①为真命题，②为假命题
• C：①为假命题，②为真命题
• D：①②都为假命题

答 案：B

解 析：一条直线与平面垂直，则直线与平面内的任意一条直线垂直，故①为真命题；二面角的两条射线必须垂直于二面角的棱，故②为假命题，因此选B选项．

2、设集合M＝{0，1，2，3，4}，N＝{1，2，3}，T＝{2，4，6}，则集合（M∩T）∪N＝（）。  

• A：{0，1，2，3，4，6}
• B：{1，2，3，4}
• C：{2，4}
• D：{2，4，6}

答 案：B

解 析：M∩T＝（2，4），则集合（M∩T）∪N＝{1，2，3，4}。答案为B。  

3、函数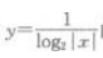定义域为（）。

• A：{z|x≠0，x∈R}
• B：{x|x≠±1，x∈R}
• C：{x|x≠0，x≠±1，x∈R}
• D：{x|x∈R}

答 案：C

解 析：|x|＞0，且|x|＝1，得x≠0，且x≠±1。答案为C。  

4、（）。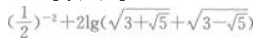

• A：3
• B：4
• C：5
• D：6

答 案：C

解 析：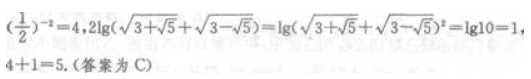

主观题

1、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：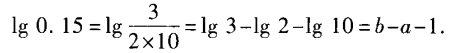

2、已知A（1，4），B（3，8），C（4，10）。求证A、B、C三点共线。  

答 案：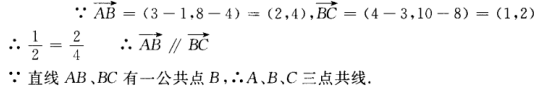

3、求下列函数的最大值、最小值和最小正周期： （1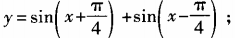）（2）y=6cosx+8sinx

答 案：  

4、cos20°cos40°cos80°的值。

答 案：

填空题

1、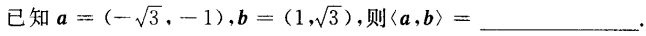  

答 案：；150°

解 析：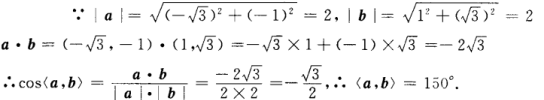

2、100件产品中有3件次品，每次抽取一件，有放回的抽取三次，恰有1件是次品的概率是______。  

答 案：0.0847

解 析：由于三次抽取是独立的，每次抽取可看做是一次试验，每次试验只有两个可能结果：“正品”或“次品”，次品率为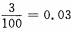，因此二次独立且重复试验恰有1件次品率为