2025年成考高起点《数学(理)》每日一练试题09月06日

2025年成考高起点《数学(理)》每日一练试题09月06日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、（）。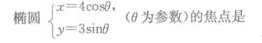

• A：（－5，0），（5，0）
• B：（0，－5），（0，5）
• C：
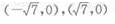
• D：

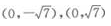
答 案：C

解 析：参数方程化成标准方程为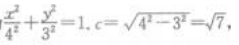

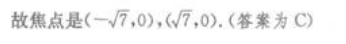
2、二项式(2x－1)⁶的展开式中，含x⁴项系数是（）。

• A：-15
• B：-240
• C：15
• D：240

答 案：D

解 析：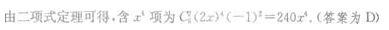

3、参数方程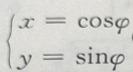（为参数）表示的图形为（）

• A：直线
• B：圆
• C：椭圆
• D：双曲线

答 案：B

解 析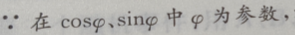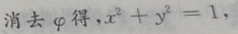：即半径为1的圆，圆心在原点

4、两个数的等差中项为20，等比中项为12，那么这两个数为（）。

• A：18，22
• B：9,16
• C：4,36
• D：16,24

答 案：C

主观题

1、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得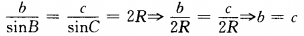

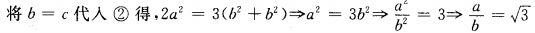
∴a：b=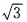：1
于是a：b：c=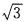：1：1。  

2、设分别讨论x→0及x→1时f（x）的极限是否存在？

答 案：∴f（x）在x=0处极限不存在 同理f（x）在x=1处极限存在

3、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

4、在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

答 案：由△ABC的面积为得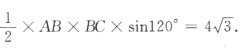所以AB =4.因此所以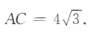

填空题

1、

答 案：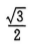

解 析：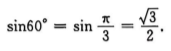

2、函数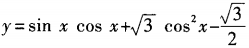（x∈R）的最小值为______。

答 案：-1

解 析：