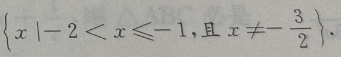2025年成考高起点《数学(理)》每日一练试题09月03日

2025年成考高起点《数学(理)》每日一练试题09月03日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、“曲线C上的点的坐标都是方程f（x，y）=0的解”是“f（x，y）=0是曲线C的方程”的（）。

• A：充分但非必要条件
• B：必要但非充分条件
• C：充要条件
• D：非充分非必要条件

答 案：B

2、（）。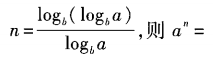

• A：1
• B：b
• C：log_ab
• D：log_ba

答 案：D

解 析：由已知，nlog_ba=log_b（log_ba），log_baⁿ=log_b（logba）， 所以aⁿ=log_ba。  

3、已知直线l：3x-2y-5=0，圆C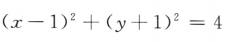：，则C上到l的距离为1的点共有（）

• A：1个
• B：2个
• C：3个
• D：4个

答 案：D

解 析：由题可知圆的圆心为（1，-1），半径为2 ，圆心到直线的距离为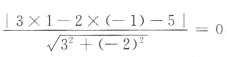,即直线过圆心，因此圆C上到直线的距离为1的点共有4个．

4、函数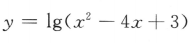的定义域是（）

• A：{x|-3＜x＜-1}
• B：{x|x＜-3或x＞-1}
• C：{x|1＜x＜3}
• D：{x|x＜1或x＞3}

答 案：D

解 析：由对数函数的性质可知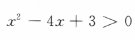，解得x＞3或x＜1，因此函数的定义域为{x|x＜1或x＞3}

主观题

1、已知x+x^-1=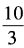，求x²+x-2的值。

答 案：由已知，得

2、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。

答 案：由已知，得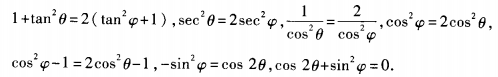

3、

答 案：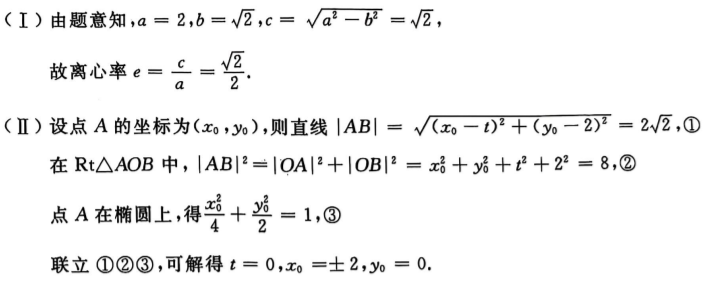

解 析：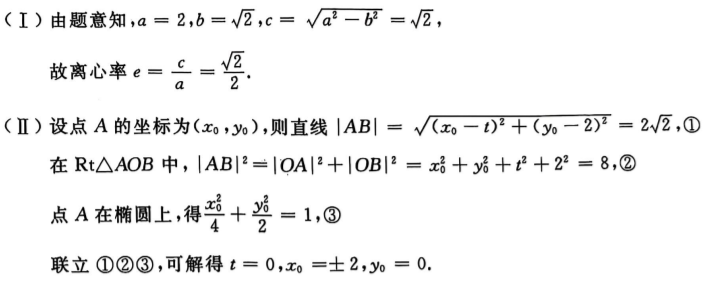

4、计算 （1）tan5°+ cot5°- 2sec80°
（2）tan15°+cot15
（3）sin15°sin75°

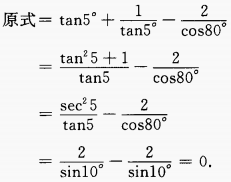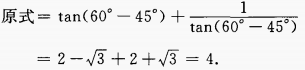答 案：（1）化切割为弦进行运算。 （2） （3）

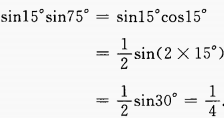
填空题

1、ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE、CE折起，使AE与BE重合如图 ，设A与B重合后的点为P，则面PCD与面ECD所成的二面角为______度，PE与面ECD成______度。

答 案：二面角为30°，PE与面ECS成60角°  

解 析：（1）求面PCD与面ECD所成的二面角为多少度，就是要求出由平面PCD与平面ECD所组成的二面角的平面角，其中画出二面角的平面角是关键，因为二面角确定以后，二面角的平面角很容易画出（由二面角的平面角的定义）。求角度时，常用到勾股定理、正弦定理、余弦定理、兰垂线定理和逆定理。 （2）求PE与面ECD成多少度，就是求直线与平面所成的角是多少度。首先要找出平面的一条斜线（直线PE）和斜线的射影，斜线和射影所成的锐角，就是直线PE和平面ECD所成的角，再求出角度。 设CD的中点为F，练PF，EF
∵PC=PD，EC=ED.
∴PF⊥CD，EF⊥CD（三垂线定理）
∠PFE是二面角P-CD-E的平面角
∵PE⊥PC，PE⊥CD.
∴PE⊥平面PCD，又PF在平面PCD内
∴PE⊥PF
设正方形边长为1（如图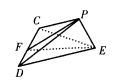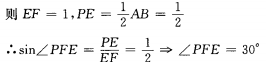） 故面PCD与面ECD所成的二面角为30°，PE与面ECS成60角°。

2、函数的定义域是（）

答 案：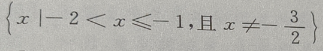

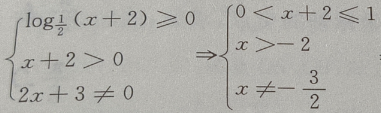
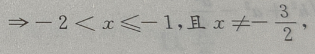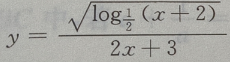解 析：所以函数的定义域是