2025年成考高起点《数学(理)》每日一练试题08月10日

2025年成考高起点《数学(理)》每日一练试题08月10日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、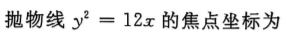

• A：(0,0)
• B：(3,0)
• C：(-3,0)
• D：(1,0)

答 案：B

解 析：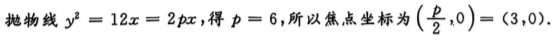

2、已知x+x^-1=2cos40°，则x⁴+x^-4=（）.  

• A：2cos20
• B：-2cos20°
• C：2sin80°
• D：-2sin80°

答 案：B

解 析：由已知得(x+x^-1)²=(2 cos 40°)²,x²+2+x^-2=4cos²40°,x²+x-²=2(2 cos²40°-1)=2cos 80°同样可得x⁴+x^-4=2 cos 160°=-2 cos 20°

3、下列各式中，不成立的是（）。

• A：
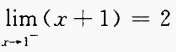
• B：
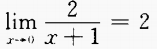
• C：
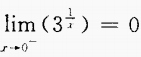
• D：

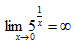
答 案：D

解 析：可用排除法，A、B、C均成立。

4、若tanα=3，则

• A：-2
• B：
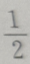
• C：2
• D：-4

答 案：A

解 析：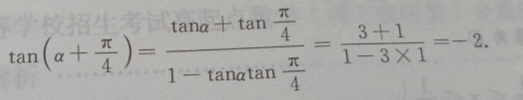

主观题

1、已知log₅3=a，log₅4=b，求log₂₅12关于a，b的表达式。  

答 案：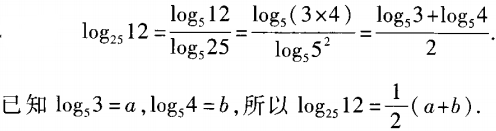

2、求（1+tan10°）（1+tan35°）的值。  

答 案：原式=1+tan10°+tan35°+tan10°·tan35°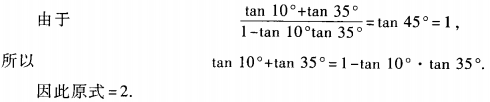

3、当自变量为何值时，函数y=2x³-3x²-12x+21有极值，其极值为多少？  

答 案：y'=6x²-6x-12=6（x-2）（x+1） 当x<-1或x>2时，y>0，当-1 故当x=-1时有极大值，其值为f（-1）=28 当x=2时有极小值，其值为f（2）=1

4、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由，得设A（x1,y1），B（x2,y2），则因此

填空题

1、若tanα-cotα=1，则=______。

答 案：4

解 析：由立方差公式得,tan³α-cot³α=(tana-cotα)(tan²α+tanαcota+cot²α)(tana-cotα)[(tanα-cotα)²+3tanαcotα]=4  

2、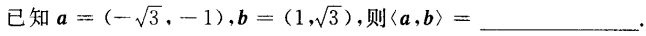  

答 案：；150°

解 析：